Số thực – Wikipedia tiếng Việt
số thực (ℝ)Kí hiệu tập hợp ( ℝ )Trong toán học, một số thực là một giá trị của một đại lượng liên tục có thể biểu thị một khoảng cách dọc theo một đường thẳng (hoặc cách khác, đại lượng có thể được biểu diễn dưới dạng khai triển thập phân vô hạn). Tính từ thực trong bối cảnh này được René Descartes giới thiệu vào thế kỷ 17, với mục đích phân biệt giữa nghiệm thực và ảo của đa thức. Các số thực bao gồm tất cả các số hữu tỷ, chẳng hạn như số nguyên −5 và phân số 4/3 và tất cả các số vô tỷ, chẳng hạn như
2
{\displaystyle {\sqrt {2}}}
R
{\displaystyle \mathbb {R} }
Các số thực hoàn toàn có thể được coi là những điểm trên một dòng dài vô hạn gọi là trục số, trong đó những điểm tương ứng với những số nguyên cách đều nhau. Bất kỳ số thực nào cũng hoàn toàn có thể được xác lập bằng cách màn biểu diễn thập phân vô hạn, ví dụ điển hình như số 8.632, trong đó mỗi chữ số liên tục được tính bằng một phần mười giá trị của số trước. Trục số thực hoàn toàn có thể được coi là một phần của mặt phẳng phức .
Số thực có thể được coi là điểm trên một trục số dài vô hạn
Bạn đang đọc: Số thực – Wikipedia tiếng Việt
Những mô tả về các số thực không đủ nghiêm ngặt theo các tiêu chuẩn hiện đại của toán học thuần túy. Việc phát hiện ra một định nghĩa phù hợp nghiêm ngặt về các con số thực sự, thực tế, việc nhận ra rằng một định nghĩa tốt hơn là cần thiết là một trong những phát triển quan trọng nhất của toán học thế kỷ 19. Định nghĩa tiên đề theo tiêu chuẩn hiện tại là các số thực tạo thành trường có thứ tự hoàn chỉnh Dedekind (R; +; ·; <), cho đến một đẳng cấu, [a] trong khi các định nghĩa xây dựng phổ biến của các số thực bao gồm khai báo chúng là tương đương các lớp trình tự Cauchy của các số hữu tỷ, cắt Dedekind hoặc biểu diễn thập phân vô hạn, cùng với các diễn giải chính xác cho các phép toán số học và quan hệ thứ tự. Tất cả các định nghĩa này đáp ứng định nghĩa tiên đề và do đó là tương đương.
Tập hợp tất cả các số thực là không thể đếm được; nghĩa là: trong khi tập hợp tất cả các số tự nhiên và các tập hợp của tất cả các số thực đều là các tập hợp vô hạn, không thể có hàm đơn ánh từ những số thực tới các số tự nhiên: lực lượng của tập hợp của tất cả các số thực (được gọi là lực lượng của continuum[5]) lớn hơn nhiều so với lực lượng của tập hợp tất cả các số tự nhiên
ℵ
0
{\displaystyle \aleph _{0}}
Tuyên bố rằng không có tập hợp con của số thực với số lượng lớn hơn tập hợp số tự nhiên và trọn vẹn nhỏ hơn tập hợp những số thực được gọi là giả thuyết continuum ( CH ). Giả thuyết này được biết là không hề chứng tỏ được và cũng không hề bác bỏ được bằng cách sử dụng những tiên đề của kim chỉ nan tập hợp Zermelo Muff Fraenkel gồm có tiên đề chọn ( ZFC ), nền tảng tiêu chuẩn của toán học tân tiến, theo nghĩa của một số ít quy mô của ZFC thỏa mãn nhu cầu CH, trong khi những quy mô khác lại vi phạm nó .
Phân số đơn thuần được sử dụng bởi người Ai Cập khoảng chừng 1000 BC ; trong ” Kinh điển Sulba ” Vệ đà ( ” Các quy tắc của hợp âm ” ), c. 600 BC, gồm có những gì hoàn toàn có thể được gọi là ” việc sử dụng ” tiên phong của số vô tỷ. Khái niệm về số vô tỷ đã được những nhà toán học Ấn Độ tiên phong đồng ý một cách ngầm định kể từ Manava ( c. 750 – 690 BC ), những người nhận thức được rằng căn bậc hai của 1 số ít số nhất định như 2 và 61 không hề được xác lập đúng chuẩn. [ 6 ] Khoảng 500 TCN, những nhà toán học Hy Lạp do Pythagoras làm chỉ huy nhận ra sự thiết yếu của những số vô tỷ, đặc biệt quan trọng là sự vô tỷ của căn bậc hai của 2 .Thời Trung cổ đã đưa ra sự gật đầu những số 0, âm, số nguyên và phân số, tiên phong bởi những nhà toán học Ấn Độ và Trung Quốc, và sau đó là những nhà toán học Ả Rập, những người tiên phong coi những số vô tỷ là những đối tượng người tiêu dùng đại số, [ 7 ] nhờ sự tăng trưởng của môn đại số. Các nhà toán học Ả Rập đã hợp nhất những khái niệm ” số ” và ” độ lớn ” thành một ý tưởng sáng tạo tổng quát hơn về những số thực. [ 8 ] Nhà toán học Ai Cập Abū Kamil Shuja ibn Aslam ( c. 850 – 930 ) là người tiên phong gật đầu số vô tỉ như những nghiệm của phương trình bậc hai hoặc như thông số trong một phương trình, thường ở dạng của căn bậc hai, căn bậc ba và căn bậc bốn. [ 9 ]Vào thế kỷ 16, Simon Stevin đã tạo ra cơ sở cho ký hiệu thập phân tân tiến và nhấn mạnh vấn đề rằng không có sự độc lạ giữa những số hữu tỷ và số vô tỷ trong yếu tố này .Vào thế kỷ 17, Descartes đã trình làng thuật ngữ ” thực ” để miêu tả nghiệm của một đa thức, phân biệt chúng với những nghiệm ” ảo ” .Trong thế kỷ 18 và 19, có nhiều khu công trình về những số vô tỷ và số siêu việt. Johann Heinrich Lambert ( 1761 ) đã đưa ra chứng tỏ sai tiên phong rằng π không hề là số hữu tỷ ; sau đó Adrien-Marie Legendre ( 1794 ) đã triển khai xong chứng tỏ này, [ 10 ] và cho thấy rằng π không phải là căn bậc hai của một số ít hữu tỷ. [ 10 ] Paolo Ruffini ( 1799 ) và Niels Henrik Abel ( 1842 ) đều đã chứng tỏ thành công xuất sắc định lý Abel-Ruffini : nội dung là phương trình bậc 5 hoặc cao hơn không hề được xử lý bằng một công thức chung chỉ gồm những phép toán cộng trừ nhân chia và khai căn .
Évariste Galois (1832) đã phát triển các kỹ thuật để xác định liệu một phương trình đã cho có thể được giải bằng phép khai căn, điều này đã tạo ra lĩnh vực của lý thuyết Galois. Joseph Liouville (1840) đã chỉ ra rằng cả e và e2 đều không thể là nghiệm số của một phương trình bậc hai có hệ số nguyên, và sau đó thiết lập sự tồn tại của các số siêu việt; Georg Cantor (1873) đã mở rộng và đơn giản hóa rất nhiều chứng minh này.[8] Charles Hermite (1873) lần đầu tiên chứng minh rằng e là số siêu việt, và Ferdinand von Lindemann (1882), chứng minh rằng π là siêu việt. Chứng minh của Lindemann đã được Weierstrass (1885) đơn giản hóa, và tiếp tục được David Hilbert (1893) đơn giản hóa tiếp, và cuối cùng đã được Adolf Hurwitz[11] và Paul Gordan đơn giản hóa đến mức độ đại số sơ cấp.[12]
Sự tăng trưởng của vi tích phân trong thế kỷ 18 đã sử dụng hàng loạt tập hợp những số thực mà không xác lập chúng rõ ràng. Định nghĩa ngặt nghèo tiên phong của số thực được Georg Cantor công bố vào năm 1871. Năm 1874, ông chứng tỏ rằng tập hợp tổng thể những số thực là vô hạn không đếm được nhưng tập hợp tổng thể những số đại số là vô hạn đếm được. Trái với niềm tin thoáng rộng, chiêu thức chứng tỏ tiên phong của ông không phải là lập luận đường chéo nổi tiếng của ông, mà ông đã xuất bản năm 1891. Xem dẫn chứng không hề đếm được tiên phong của Cantor .
Hệ thống số thực
(
R
;
+
;
⋅
;
<){\displaystyle (\mathbb {R} ;{}+{};{}\cdot {};{}<{})}
Mục Lục
Tiếp cận dùng tiên đề[sửa|sửa mã nguồn]
Tập hợp R { \ displaystyle \ mathbb { R } } là tập hợp toàn bộ những số thực, mà thỏa mãn nhu cầu những điều kiện kèm theo sau :
Thuộc tính cuối cùng là thứ phân biệt số thực với số hữu tỷ (và với các trường khác có thứ tự kỳ lạ hơn). Ví dụ,
{
x
∈
Q
:
x
2
<2}{\displaystyle \{x\in \mathbb {Q} :x^{2}<2\}}
2
{\displaystyle {\sqrt {2}}}
không phải là số hữu tỷ.
Các thuộc tính này ngụ ý thuộc tính Archimedes (không được ngụ ý bởi các định nghĩa khác về tính đầy đủ), cho biết rằng tập hợp các số nguyên không có giới hạn trên trong số thực. Trên thực tế, nếu điều này là sai, thì các số nguyên sẽ có giới hạn trên N nhỏ nhất; khi đó, N – 1 sẽ không là giới hạn trên và sẽ có một số nguyên n sao cho n > N – 1, và do đó n + 1 > N, điều này mâu thuẫn với thuộc tính giới hạn trên của N.
Các số thực được chỉ định duy nhất bởi các thuộc tính trên. Chính xác hơn, với bất kỳ hai trường có thứ tự hoàn chỉnh Dedekind
R
1
{\displaystyle \mathbb {R} _{1}}
R
2
{\displaystyle \mathbb {R} _{2}}
R
1
{\displaystyle \mathbb {R} _{1}}
đến
R
2
{\displaystyle \mathbb {R_{2}} }
. Tính duy nhất này cho phép chúng ta nhìn nhận về chúng về cơ bản là cùng một đối tượng toán học.Đối với một tiên đề khác về R { \ displaystyle \ mathbb { R } }, hãy xem tiên đề của Tarski về số thực .
Xây dựng từ những số hữu tỉ[sửa|sửa mã nguồn]
Các số thực hoàn toàn có thể được kiến thiết xây dựng như một sự hoàn hảo hóa những số hữu tỉ, theo cách mà một dãy được xác lập bằng khai triển thập phân hoặc nhị phân như ( 3 ; 3.1 ; 3.14 ; 3.141 ; 3.1415 ; … ) quy tụ thành 1 số ít thực duy nhất — Trong trường hợp này là π. Để biết cụ thể và những cấu trúc khác của số thực, hãy xem cấu trúc của số thực .
Các đặc thù cơ bản[sửa|sửa mã nguồn]
Chính thức hơn, những số thực có hai thuộc tính cơ bản là trường có thứ tự và có thuộc tính cận trên thấp nhất. Thuộc tính tiên phong nói rằng những số thực gồm có một trường, với phép cộng và phép nhân cũng như phép chia cho những số khác không, hoàn toàn có thể được sắp xếp trọn vẹn trên một trục số theo cách thích hợp với phép cộng và phép nhân. Thuộc tính thứ hai nói rằng, nếu một tập hợp những số thực không trống có số lượng giới hạn trên, thì nó có cận trên là số thực nhỏ nhất. Điều kiện thứ hai phân biệt những số thực với những số hữu tỷ : ví dụ : tập hợp những số hữu tỷ có bình phương nhỏ hơn 2 là tập hợp có số lượng giới hạn trên ( ví dụ 1,5 ) nhưng không có cận trên tối thiểu ( là số hữu tỷ ) : do đó những số hữu tỷ không phân phối những đặc thù có cận trên nhỏ nhất .
Tính hoàn hảo[sửa|sửa mã nguồn]
Một nguyên do chính cho việc sử dụng số thực là nhiều dãy số có số lượng giới hạn không hữu tỷ. Về mặt hình thức hơn, những số thực là hoàn hảo ( theo nghĩa của khoảng trống số liệu hoặc khoảng trống như nhau, nghĩa là khác với tính hoàn hảo Dedekind của thứ tự trong phần trước ) :
Một dãy (xn) gồm các số thực được gọi là dãy Cauchy nếu với bất kỳ ε > 0 nào tồn tại số nguyên N (có thể phụ thuộc vào ε) sao cho khoảng cách |xn − xm| nhỏ hơn ε với mọi n và m đều lớn hơn N. Định nghĩa này, ban đầu được Cauchy đưa ra, chuẩn hóa thực tế rằng xn cuối cùng tiến đến và gần sát nhau một cách tùy ý.
Một dãy (xn) hội tụ đến giới hạn x nếu các phần tử của nó cuối cùng đến và tiếp tục gần với x một cách tùy ý, nghĩa là, nếu với bất kỳ ε > 0 thì tồn tại một số nguyên N (có thể phụ thuộc vào ε) sao cho khoảng cách |xn − x| nhỏ hơn ε với mọi n lớn hơn N.
Mọi dãy quy tụ là một dãy Cauchy, và điều ngược lại đúng với những số thực, và điều này có nghĩa là khoảng trống tôpô của những số thực là hoàn hảo .Tập hợp những số hữu tỉ là không vừa đủ. Ví dụ, dãy ( 1 ; 1.4 ; 1.41 ; 1.414 ; 1.4142 ; 1.41421 ; … ), trong đó mỗi số hạng thêm một chữ số của khai triển thập phân của căn bậc hai dương của 2, là dãy Cauchy nhưng nó không quy tụ thành một số ít hữu tỉ ( ngược lại, trong tập hợp những số thực, nó quy tụ về căn bậc hai dương của 2 ) .Tính chất không thiếu của những số thực là cơ sở để kiến thiết xây dựng phép vi tích phân, và nói chung là giải tích toán học. Đặc biệt, việc kiểm tra rằng một dãy là một dãy Cauchy được cho phép chứng tỏ rằng một dãy có số lượng giới hạn, mà không cần đo lường và thống kê số lượng giới hạn này, và thậm chí còn không cần biết về nó .Ví dụ, chuỗi tiêu chuẩn của hàm mũ
e
x
=
∑
n
=
0
∞
x
n
n
!
{\displaystyle e^{x}=\sum _{n=0}^{\infty }{\frac {x^{n}}{n!}}}
hội tụ tới một số thực với mọi x, vì tổng
∑
n
=
N
M
x
n
n
!
{\displaystyle \sum _{n=N}^{M}{\frac {x^{n}}{n!}}}
có thể được làm nhỏ tùy ý (không phụ thuộc vào M) bằng cách chọn N đủ lớn. Điều này chứng tỏ rằng chuỗi này là một chuỗi Cauchy, và do đó hội tụ, cho thấy rằng
e
x
{\displaystyle e^{x}}
” Trường được xếp thứ tự hoàn hảo “[sửa|sửa mã nguồn]
Các số thực thường được diễn đạt là ” trường có thứ tự hoàn hảo “, một cụm từ hoàn toàn có thể được hiểu theo nhiều cách .
Đầu tiên, một thứ tự có thể là hoàn thành bên trong nó. Dễ dàng nhận thấy rằng không có trường có thứ tự nào có thể là hoàn chỉnh bên trong nó, bởi vì nó không thể có phần tử lớn nhất (với bất kỳ phần tử z, z+1 là lớn hơn).
Ngoài ra, một thứ tự hoàn toàn có thể là hoàn hảo Dedekind .
Hai khái niệm về tính hoàn chỉnh này bỏ qua cấu trúc trường. Tuy nhiên, một nhóm có thứ tự (trong trường hợp này là nhóm phụ gia của trường) xác định cấu trúc đồng nhất, và cấu trúc đồng nhất có khái niệm về tính hoàn chỉnh là một trường hợp đặc biệt. (việc đề cập đến khái niệm đầy đủ trong không gian đồng nhất hơn là khái niệm có liên quan và được biết đến nhiều hơn cho không gian mêtric, vì định nghĩa của không gian metric dựa trên việc đã có đặc điểm của các số thực.)
R
{\displaystyle \mathbb {R} }
không phải là trường có thứ tự hoàn chỉnh thống nhất duy nhất, nhưng nó là trường Archimedes hoàn chỉnh đồng nhất duy nhất, và thực sự người ta thường nghe thấy cụm từ “trường Archimedes hoàn chỉnh” thay vì “trường có thứ tự hoàn chỉnh”. Mọi trường Archimedes hoàn chỉnh đồng nhất cũng phải là trường hoàn chỉnh Dedekind (và ngược lại). Cảm giác đầy đủ này có liên quan chặt chẽ nhất đến việc xây dựng các thực từ các chuỗi Cauchy (việc xây dựng được thực hiện đầy đủ trong bài viết này), vì nó bắt đầu với trường Archimedean (các số hữu tỷ) và tạo thành sự hoàn thành đồng nhất của nó theo một cách tiêu chuẩn.
Nhưng cách sử dụng ban đầu của cụm từ “trường Archimedes hoàn chỉnh” là của David Hilbert, người có hàm ý với ý nghĩa khác. Ý của Hilbert là các số thực tạo thành trường Archimedes lớn nhất theo nghĩa là mọi trường Archimedes khác là một trường con của
R
{\displaystyle \mathbb {R} }
. Như vậy
R
{\displaystyle \mathbb {R} }
là “hoàn chỉnh” theo nghĩa là không thể thêm gì nữa mà không làm cho nó không còn là một trường Archimedes. Cảm giác đầy đủ này có liên quan chặt chẽ nhất đến việc xây dựng các số thực từ các số siêu thực, vì việc xây dựng đó bắt đầu với một lớp thích hợp chứa mọi trường có thứ tự (số siêu thực) và sau đó chọn từ đó trường con Archimedes lớn nhất.
Các đặc thù nâng cao[sửa|sửa mã nguồn]
Các số thực là không thể đếm được; nghĩa là, có nhiều số thực hơn số tự nhiên, mặc dù cả hai tập hợp này đều là vô hạn. Trên thực tế, bản số của số thực bằng với bản số của các tập hợp con (tức là tập hợp lũy thừa) của các số tự nhiên, và lập luận đường chéo của Cantor nói rằng bản số của tập hợp sau lớn hơn hẳn so với bản số của
N
{\displaystyle \mathbb {N} }
Là một khoảng trống tôpô, những số thực hoàn toàn có thể phân tách được. Điều này là do tập hợp những số hữu tỉ, hoàn toàn có thể đếm được, sum sê nằm trong những số thực. Các số vô tỉ cũng rậm rạp trong những số thực, tuy nhiên chúng không đếm được và có cùng số lượng với số thực .
Các số thực tạo thành một không gian mêtric: khoảng cách giữa x và y được xác định là giá trị tuyệt đối |x − y|. Do là một tập hợp có thứ tự hoàn toàn, chúng cũng mang một cấu trúc liên kết thứ tự; cấu trúc liên kết phát sinh từ số liệu và cấu trúc liên kết phát sinh từ thứ tự giống hệt nhau, nhưng mang lại các trình bày khác nhau cho cấu trúc liên kết — trong cấu trúc liên kết thứ tự là các khoảng có thứ tự, trong cấu trúc liên kết số liệu là epsilon-ball. Cấu trúc cắt Dedekind sử dụng trình bày cấu trúc liên kết thứ tự, trong khi cấu trúc trình tự Cauchy sử dụng trình bày cấu trúc liên kết số liệu. Các thực tạo thành một không gian số liệu có thể co lại (do đó được kết nối và kết nối đơn giản), có thể phân tách và hoàn chỉnh với số chiều Hausdorff là 1. Các số thực là compact cục bộ nhưng không compact. Có nhiều thuộc tính khác nhau chỉ định duy nhất chúng; ví dụ, tất cả các cấu trúc liên kết thứ tự không bị ràng buộc, được kết nối và có thể phân tách nhất thiết phải là đồng phôi với các số thực.
Mọi số thực không âm đều có căn bậc hai thuộc
R
{\displaystyle \mathbb {R} }
, mặc dù không có số âm nào có căn bậc hai thuộc
R
{\displaystyle \mathbb {R} }
. Điều này cho thấy rằng thứ tự trên
R
{\displaystyle \mathbb {R} }
được xác định bởi cấu trúc đại số của nó. Ngoài ra, mọi đa thức bậc lẻ đều có ít nhất một nghiệm là số thực: hai thuộc tính này làm cho
R
{\displaystyle \mathbb {R} }
trở thành ví dụ hàng đầu về một trường đóng thực. Chứng minh tính chất này là nửa đầu tiên của một chứng minh của định lý cơ bản của đại số.
Xem thêm: “Không” có ý nghĩa gì?
Các số thực có một số đo chính tắc, số đo Lebesgue, là số đo Haar trên cấu trúc của chúng như một nhóm tôpô được chuẩn hóa sao cho khoảng chừng đơn vị chức năng [ 0 ; 1 ] có số đo là 1. Tồn tại những tập hợp số thực mà Lebesgue không hề đo lường và thống kê được, ví dụ : Tập hợp Vitali .Tiên đề cận trên lớn nhất về số thực đề cập đến những tập con của số thực và do đó là một câu lệnh logic bậc hai. Không thể đặc trưng cho những số thực chỉ với logic bậc nhất : định lý Löwenheim – Skolem ý niệm rằng sống sót một tập con chi chít hoàn toàn có thể đếm được của những số thực thỏa mãn nhu cầu đúng chuẩn những câu trong logic bậc nhất như chính những số thực. Tập hợp những số siêu thực thỏa mãn nhu cầu những câu thứ tự bậc nhất giống như R { \ displaystyle \ mathbb { R } }. Các trường có thứ tự cung ứng những câu thứ tự tiên phong giống như R { \ displaystyle \ mathbb { R } } được gọi là quy mô không tiêu chuẩn của R { \ displaystyle \ mathbb { R } }. Điều này là những gì làm cho nghiên cứu và phân tích không tiêu chuẩn hoạt động giải trí ; bằng cách chứng tỏ một câu lệnh bậc nhất trong một số ít quy mô không chuẩn ( hoàn toàn có thể thuận tiện hơn việc chứng tỏ nó trong R { \ displaystyle \ mathbb { R } } ), khi đó tất cả chúng ta hiểu rằng công bố tựa như cũng phải đúng với R { \ displaystyle \ mathbb { R } } .
Trường số thực
R
{\displaystyle \mathbb {R} }
là một trường mở rộng của trường số hữu tỉ
Q
{\displaystyle \mathbb {Q} }
R
{\displaystyle \mathbb {R} }
do đó có thể được xem như một không gian vectơ trên
Q
{\displaystyle \mathbb {Q} }
. Lý thuyết tập hợp Zermelo – Fraenkel với tiên đề lựa chọn đảm bảo sự tồn tại của cơ sở của không gian vectơ này: tồn tại một tập hợp B gồm các số thực sao cho mọi số thực có thể được viết duy nhất dưới dạng một tổ hợp tuyến tính hữu hạn của các phần tử của tập hợp này, sử dụng chỉ các hệ số hữu tỉ, và sao cho không phần tử nào của B là tổ hợp tuyến tính hữu tỉ của các phần tử khác. Tuy nhiên, định lý tồn tại này hoàn toàn là lý thuyết, vì một cơ sở như vậy chưa bao giờ được mô tả một cách rõ ràng.
Định lý sắp xếp tốt ý niệm rằng những số thực hoàn toàn có thể được sắp xếp hài hòa và hợp lý nếu tiên đề lựa chọn được giả định : sống sót một thứ tự hàng loạt trên R { \ displaystyle \ mathbb { R } } với thuộc tính mà mọi tập hợp con không trống của R { \ displaystyle \ mathbb { R } } có một thành phần nhỏ nhất trong thứ tự này. ( Thứ tự tiêu chuẩn ≤ của những số thực không phải là một thứ tự tốt vì ví dụ một khoảng chừng mở không chứa thành phần nhỏ nhất trong thứ tự này. ) Một lần nữa, sự sống sót của một trật tự tốt như vậy trọn vẹn là triết lý, vì nó chưa được diễn đạt rõ ràng. Nếu giả sử V = L cùng với những tiên đề của ZF, thứ tự tốt của những số thực hoàn toàn có thể được xác lập một cách rõ ràng bằng một công thức. [ 13 ]Một số thực hoàn toàn có thể thống kê giám sát được hoặc không hề đo lường và thống kê được ; dù cho là giám sát ngẫu nhiên về mặt thuật toán hoặc không ; và ngẫu nhiên về mặt số học hoặc không .
Ứng dụng và liên kết với những nghành khác[sửa|sửa mã nguồn]
Số thực và logic[sửa|sửa mã nguồn]
Các số thực thường được chuẩn tắc hóa bằng cách sử dụng tiên đề Zermelo-Fraenkel của triết lý tập hợp, nhưng một số ít nhà toán học điều tra và nghiên cứu những số thực bằng những cơ sở logic khác của toán học. Đặc biệt, những số thực còn được điều tra và nghiên cứu trong toán học đảo ngược và toán học thiết kế. [ 14 ]Các số siêu thực được tăng trưởng bởi Edwin Hewitt, Abraham Robinson và những người khác lan rộng ra tập hợp những số thực bằng cách trình làng những số vô hạn và vô hạn, được cho phép kiến thiết xây dựng phép tính thập phân theo cách thân mật hơn với trực giác khởi đầu của Leibniz, Euler, Cauchy và những người khác .Lý thuyết tập hợp bên trong của Edward Nelson đã làm phong phú và đa dạng thêm triết lý tập hợp Zermelo-Fraenkel về mặt cú pháp bằng cách trình làng một vị từ một ngôi ” tiêu chuẩn “. Theo cách tiếp cận này, những số tương tự là thành phần ( không phải ” tiêu chuẩn ” ) của tập hợp những số thực ( chứ không phải là thành phần của phần lan rộng ra của chúng, như trong kim chỉ nan của Robinson ) .
Giả thuyết continuum cho rằng bản số của tập hợp các số thực là
ℵ
1
{\displaystyle \aleph _{1}}
ℵ
0
{\displaystyle \aleph _{0}}
, bản số của các số nguyên. Paul Cohen đã chứng minh vào năm 1963 rằng nó là một tiên đề độc lập với các tiên đề khác của lý thuyết tập hợp; nghĩa là: người ta có thể chọn giả thuyết liên tục hoặc phủ định của nó như một tiên đề của lý thuyết tập hợp, mà không có mâu thuẫn.
Trong vật lý[sửa|sửa mã nguồn]
Trong khoa học vật lý, hầu hết những hằng số vật lý như hằng số mê hoặc phổ quát và những biến vật lý, ví dụ điển hình như vị trí, khối lượng, vận tốc và điện tích, được quy mô hóa bằng cách sử dụng số thực. Trên trong thực tiễn, những kim chỉ nan vật lý cơ bản như cơ học cổ xưa, điện từ học, cơ học lượng tử, thuyết tương đối rộng và quy mô chuẩn được miêu tả bằng cách sử dụng những cấu trúc toán học, nổi bật là đa tạp trơn hoặc khoảng trống Hilbert, dựa trên những số thực, mặc dầu những phép đo thực tiễn của những đại lượng vật lý có độ đúng mực hữu hạn .Các nhà vật lý nhiều lúc gợi ý rằng một kim chỉ nan cơ bản hơn sẽ sửa chữa thay thế những số thực bằng những đại lượng không tạo thành một continuum, nhưng những yêu cầu như vậy vẫn mang tính suy đoán. [ 15 ]
Trong giám sát[sửa|sửa mã nguồn]
Với 1 số ít ngoại lệ, hầu hết những máy tính không hoạt động giải trí trên số thực. Thay vào đó, chúng hoạt động giải trí với những phép giao động đúng chuẩn hữu hạn được gọi là số dấu phẩy động. Trên trong thực tiễn, hầu hết những phép tính khoa học đều sử dụng số học dấu phẩy động. Các số thực thỏa mãn nhu cầu những quy tắc thường thì của số học, nhưng số dấu phẩy động thì không .
Máy tính không thể lưu trữ trực tiếp các số thực tùy ý có vô số chữ số. Độ chính xác có thể đạt được bị giới hạn bởi số lượng bit được phân bổ để lưu trữ một số, cho dù là số dấu phẩy động hay số có độ chính xác tùy ý. Tuy nhiên, các hệ thống đại số máy tính có thể hoạt động chính xác trên các đại lượng vô tỉ bằng cách thao tác các công thức cho chúng (chẳng hạn như
2
,
{\displaystyle {\sqrt {2}},}
arcsin
(
2
/
23
)
,
{\displaystyle \arcsin(2/23),}
∫
0
1
x
x
d
x
{\displaystyle \textstyle \int _{0}^{1}x^{x}\,dx}
Một số thực được gọi là có thể tính toán được nếu tồn tại một thuật toán đưa ra các chữ số của nó. Bởi vì chỉ có nhiều thuật toán có thể đếm được[17] nhưng một số thực là không đếm được, hầu như tất cả các số thực đều không thể tính toán được. Hơn nữa, sự bằng nhau của hai số có thể tính toán được là một vấn đề không thể giải quyết được. Một số nhà toán học kiến tạo chỉ chấp nhận sự tồn tại của những số thực mà có thể tính toán được. Tập hợp các số có thể xác định được rộng hơn, nhưng vẫn chỉ có thể đếm được.
Số thực trong kim chỉ nan tập hợp[sửa|sửa mã nguồn]
Trong triết lý tập hợp, đơn cử là triết lý tập hợp miêu tả, khoảng trống Baire được sử dụng làm đại diện thay mặt cho những số thực vì sau này có 1 số ít thuộc tính tôpô ( tính liên thông ) gây phiền phức về kỹ thuật. Các thành phần của khoảng trống Baire được gọi là ” những số thực ” .
Các phép toán[sửa|sửa mã nguồn]
- R × R ↦ R { \ displaystyle \ mathbb { R } \ times \ mathbb { R } \, \ mapsto \, \ mathbb { R } }
đóng trên R { \ displaystyle \ mathbb { R } }
- ( a, b ) ↦ a + b { \ displaystyle \ left ( a, \, b \ right ) \, \ mapsto \, a + b }
Sao cho :
- ∀ a ∈ R : a + 0 = a { \ displaystyle \ forall \, \, a \, \ in \, \ mathbb { R } : a + 0 = a }
- ∀ a, b ∈ R : a + b = ( a + b ) { \ displaystyle \ forall \, \, a, \, b \, \ in \, \ mathbb { R } : a + b = \ left ( a + b \ right ) }
- ∀ a ∈ R : a + 0 = a { \ displaystyle \ forall \, \, a \, \ in \, \ mathbb { R } : a + 0 = a }
Có thể thấy phép cộng xác lập như trên là sống sót và duy nhất .Ngoài ra, ta còn hoàn toàn có thể chứng tỏ được rằng :
- ∀ a, b ∈ R : a + b = b + a { \ displaystyle \ forall \, \, a, \, b \, \ in \, \ mathbb { R } : a + b = b + a }
- ∀ a, b, c ∈ R : ( a + b ) + c = a + ( b + c ) { \ displaystyle \ forall \, \, a, \, b, \, c \, \ in \, \ mathbb { R } : \ left ( a + b \ right ) + c = a + \ left ( b + c \ right ) }
- ∀ a, b, c ∈ R : a + c = b + c ⇒ a = b { \ displaystyle \ forall \, \, a, \, b, \, c \, \ in \, \ mathbb { R } : a + c = b + c \, \ Rightarrow \, a = b }
Giá trị tuyệt đối của số thực a là khoảng cách từ điểm a đến 0 trên trục số thực và kí hiệu là | a |. ( Đọc là : Giá trị tuyệt đối của a ). Lưu ý : Giá trị tuyệt đối của số thực a luôn được hiệu quả là một số ít lớn hơn hoặc bằng 0 .
Các tập hợp số[sửa|sửa mã nguồn]
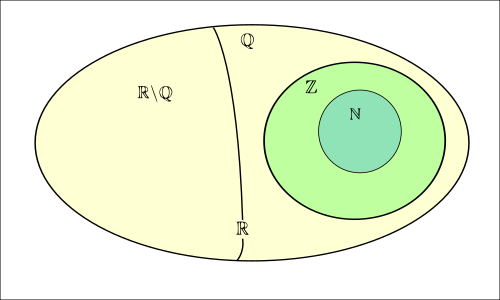Tập hợp số thực
Ngoài ra, một số ít thực hoàn toàn có thể là số đại số hoặc số siêu việt .
Tập hợp số thực là tập hợp con của số phức
x
=
a
+
b
i
{\displaystyle x=a+bi}
b
=
0
{\displaystyle b=0}
Các tập hợp con trên Tập hợp những số thực[sửa|sửa mã nguồn]
Khoảng :
R
=
(
−
∞
,
∞
)
{\displaystyle \mathbb {R} =\left(-\infty ,\,\infty \right)}
Ví dụ :
x
∈
N
∗
⇔
x
∈
(
0
,
∞
)
{\displaystyle x\in \mathbb {N} ^{*}\Leftrightarrow \,x\in \left(0,\,\infty \right)}
Đoạn :
A
=
[
3
,
5
]
⇔
A
=
{
x
∣
3
≤
x
≤
5
}
{\displaystyle {\text{A}}=\left[3,\,5\right]\,\Leftrightarrow \,{\text{A}}=\left\{x\mid 3\leq x\leq 5\right\}}
![{\displaystyle {\text{A}}=\left[3,\,5\right]\,\Leftrightarrow \,{\text{A}}=\left\{x\mid 3\leq x\leq 5\right\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/489fa34ae8c96e18ef40f8b6010212428cebc4af)
Nửa khoảng chừng :
x
∈
N
⇔
x
∈
[
0
,
∞
)
{\displaystyle x\in \mathbb {N} \,\Leftrightarrow \,x\in \left[0,\,\infty \right)}
Xem thêm: “Không” có ý nghĩa gì?
Chú ý:
∞ đọc là vô cực .
- ^
Chính xác hơn, với hai trường hoàn toàn được sắp xếp hoàn toàn, có một đẳng hình độc đáo giữa chúng. Điều này ngụ ý rằng danh tính là tự hình trường độc đáo của thực tế tương thích với thứ tự.
Liên kết ngoài[sửa|sửa mã nguồn]
Source: https://dvn.com.vn
Category: Hỏi Đáp
