Mục Lục

Tập hợp (toán học) – Các phần tử tạo nên một tập hợp

Trong toán học, một tập hợp là một bộ các phần tử.[1][2][3] Các phần tử tạo nên một tập hợp có thể là bất kỳ loại đối tượng toán học nào: số, ký hiệu, điểm trong không gian, đường thẳng, các hình dạng hình học khác, các biến hoặc thậm chí các tập hợp khác. Tập hợp không có phần tử nào là tập hợp rỗng ; một tập hợp với một phần tử duy nhất là một đơn điểm. Một tập hợp có thể có một số phần tử hữu hạn hoặc là một tập hợp vô hạn. Hai tập hợp bằng nhau khi và chỉ khi chúng có chính xác các phần tử giống nhau.[5]

Một tập hợp trong toán học là một tập hợp các phần tử, và các phần tử này có thể là bất kỳ thứ gì, miễn là chúng có một đặc điểm chung cụ thể mà bạn muốn xem xét hoặc nghiên cứu. Dưới đây là một số ví dụ về các phần tử có thể tạo nên một tập hợp:

Số nguyên: Tập hợp số nguyên bao gồm tất cả các số nguyên, bao gồm số nguyên dương, số nguyên âm, và số nguyên không.
Số tự nhiên: Tập hợp số tự nhiên bao gồm tất cả các số từ 1 trở đi (1, 2, 3, 4, …).
Tập hợp các chữ cái trong bảng chữ cái tiếng Anh: Tập hợp này bao gồm các chữ cái từ “A” đến “Z”, hoặc từ “a” đến “z”.
Tập hợp các số nguyên tố: Tập hợp này chứa tất cả các số nguyên tố, chẳng hạn như 2, 3, 5, 7, 11, và nhiều số nguyên tố khác.
Tập hợp các màu sắc: Tập hợp này có thể bao gồm tất cả các màu sắc khác nhau, chẳng hạn như đỏ, xanh, vàng, và màu tím.
Tập hợp các động vật: Tập hợp này có thể chứa các loài động vật như chó, mèo, hổ, và cừu.
Tập hợp các hình học: Tập hợp này có thể bao gồm các hình học như tam giác, hình vuông, hình tròn, và hình chữ nhật.

Như vậy, các phần tử tạo nên một tập hợp có thể là bất kỳ thứ gì, và tùy thuộc vào mục đích của bạn, tập hợp này có thể được xác định và sắp xếp theo cách khác nhau. Tập hợp là một khái niệm cơ bản trong toán học và được sử dụng rộng rãi trong nhiều lĩnh vực khác nhau của ngành này.

Tập hợp xuất hiện khắp nơi trong toán học văn minh. Thật vậy, triết lý tập hợp, đơn cử hơn là kim chỉ nan tập hợp Zermelo-Fraenkel, đã là giải pháp tiêu chuẩn để phân phối nền tảng ngặt nghèo cho tổng thể những phân nhánh của toán học kể từ nửa đầu thế kỷ 20 .

Khái niệm tập hợp xuất hiện trong toán học vào cuối thế kỷ 19.[6] Từ tập hợp trong tiếng Đức, Menge, được Bernard Bolzano đặt ra trong tác phẩm Paradoxes of the Infinite.[7][8][9]

Menge cho tập hợp được dịch với nghĩa aggregate ở đây.

Đoạn văn có bản dịch từ định nghĩa gốc của Georg Cantor. Từ tiếng Đứcchođược dịch với nghĩaở đây.

Bạn đang đọc: Tập hợp (toán học) – Wikipedia tiếng Việt

Georg Cantor, một trong những người sáng lập ra lý thuyết tập hợp, đã đưa ra định nghĩa sau đây ở đầu cuốn sách Beiträge zur Begründung der transfiniten Mengenlehre:[10]

Tập hợp là sự gộp lại với nhau thành một toàn diện và tổng thể những đối tượng người dùng xác lập, riêng không liên quan gì đến nhau của nhận thức hoặc tâm lý của tất cả chúng ta — được gọi là những thành phần của tập hợp .

Bertrand Russell gọi một tập hợp là một lớp: “Khi các nhà toán học xử lý những gì họ gọi là đa tạp, tổng hợp, Menge, tổ hợp hoặc một số tên tương đương, thì điều đó là phổ biến, đặc biệt là khi số lượng các thuật ngữ liên quan là hữu hạn, coi đối tượng được đề cập. (thực tế là một lớp) được xác định bằng cách liệt kê các thuật ngữ của nó, và có thể bao gồm một thuật ngữ duy nhất, trong trường hợp đó là lớp.”[11]

Lý thuyết tập hợp ngây thơ[sửa|sửa mã nguồn]

Thuộc tính quan trọng nhất của một tập hợp là nó có thể có các phần tử. Hai tập hợp bằng nhau khi chúng có các phần tử giống nhau. Chính xác hơn, tập A và B là bằng nhau nếu mọi phần tử của A là phần tử của B, và mọi phần tử của B là một phần tử của A ; thuộc tính này được gọi là tính mở rộng của các tập hợp.

Khái niệm đơn thuần về một tập hợp đã tỏ ra vô cùng có ích trong toán học, nhưng nghịch lý lại phát sinh nếu không có số lượng giới hạn nào được đặt ra về cách những tập hợp hoàn toàn có thể được thiết kế xây dựng :

Nghịch lý Russell cho thấy rằng “tập hợp của tất cả các tập hợp không chứa chính chúng“, tức là, {x|x là một tập hợp và x ∉ x}, không thể tồn tại.
Nghịch lý Cantor cho thấy “tập hợp của tất cả các tập hợp” không thể tồn tại.

Lý thuyết tập hợp ngây thơ định nghĩa một tập hợp là bất kỳ tập hợp được xác định rõ ràng của các phần tử riêng biệt, nhưng các vấn đề nảy sinh từ sự mơ hồ của thuật ngữ được xác định rõ ràng.

Lý thuyết tập hợp tiên đề[sửa|sửa mã nguồn]

Trong những nỗ lực tiếp theo để xử lý những nghịch lý này kể từ thời gian hình thành triết lý tập hợp sơ khai khởi đầu, những đặc thù của tập hợp đã được xác lập bởi những tiên đề. Thuyết tập hợp tiên đề lấy khái niệm tập hợp làm khái niệm sơ khai. [ 13 ] Mục đích của tiên đề là phân phối một khuôn khổ cơ bản để từ đó suy ra tính đúng hay sai của những mệnh đề toán học đơn cử ( phát biểu ) về tập hợp, sử dụng logic bậc nhất. Tuy nhiên, theo những định lý về tính không không thiếu của Gödel, không hề sử dụng logic bậc nhất để chứng tỏ bất kể triết lý tập tiên đề đơn cử nào mà không có nghịch lý .

Cách những tập hợp được xác lập và thiết lập ký hiệu[sửa|sửa mã nguồn]

Các sách báo toán học thường biểu thị tập hợp bằng chữ in hoa[14][15] in nghiêng, chẳng hạn như A, B, C[15][16] Một tập hợp cũng có thể được gọi là tập hợp hoặc họ, đặc biệt là khi bản thân các phần tử của nó lại là các tập hợp.

Ký hiệu list[sửa|sửa mã nguồn]

Kí hiệu danh sách hoặc bảng liệt kê xác định một tập hợp bằng cách liệt kê các phần tử của nó giữa các dấu ngoặc nhọn, được phân tách bằng dấu phẩy:[17][18][19][20]

A = {4, 2, 1, 3}

Trong một tập hợp, tổng thể những gì quan trọng là liệu mỗi thành phần có nằm trong đó hay không, vì thế thứ tự của những thành phần trong ký hiệu list là không tương quan ( ngược lại, trong một chuỗi, một bộ hoặc một hoán vị của một tập hợp, thứ tự của những thành phần là quan trọng ). [ 16 ] [ 21 ] [ 22 ]Đối với những tập hợp có nhiều thành phần, đặc biệt quan trọng là những tập hợp theo một mẫu không tường minh, list những thành phần hoàn toàn có thể được viết tắt bằng cách sử dụng dấu chấm lửng ‘ … ‘. [ 23 ] [ 24 ] Ví dụ : tập hợp 1000 số nguyên dương tiên phong hoàn toàn có thể được chỉ định trong bảng liệt kê như{ 1, 2, 3, …, 1000 }

Tập hợp vô hạn trong ký hiệu list[sửa|sửa mã nguồn]

Tập hợp vô hạn là tập hợp có list vô tận những thành phần. Để miêu tả một tập hợp vô hạn trong ký hiệu list, một dấu chấm lửng được đặt ở cuối list hoặc ở cả hai đầu, để chỉ ra rằng list liên tục mãi mãi. Ví dụ : tập hợp những số nguyên không âm là{ 0, 1, 2, 3, 4, … } ,và tập hợp toàn bộ những số nguyên là{ …, − 3, − 2, − 1, 0, 1, 2, 3, … } .

Định nghĩa ngữ nghĩa[sửa|sửa mã nguồn]

Một cách khác để xác lập một tập hợp là sử dụng quy tắc để xác lập những thành phần là gì :

Gọi A là tập hợp có các phần tử là bốn số nguyên dương đầu tiên.

Gọi B là tập hợp các màu của lá cờ Pháp.

Định nghĩa như vậy được gọi là mô tả ngữ nghĩa.[26]

Ký hiệu cách tạo tập hợp[sửa|sửa mã nguồn]

Ký hiệu cách tạo tập hợp chỉ định một tập hợp là một lựa chọn từ một tập hợp lớn hơn, được xác lập bởi một điều kiện kèm theo trên những thành phần. [ 26 ] [ 27 ] [ 28 ] Ví dụ, một tập F hoàn toàn có thể được định nghĩa như sau :

=
{
n
∣
n

là một số nguyên, và

0
≤
n
≤
19
}
.

{\displaystyle =\{n\mid n{\text{ là một số nguyên, và }}0\leq n\leq 19\}.}

$=\{n\mid n{\text{ là một số nguyên, và }}0\leq n\leq 19\}.$

Trong ký hiệu này, thanh dọc ” | ” có nghĩa là ” sao cho “, và miêu tả hoàn toàn có thể được hiểu là ” F là tập hợp toàn bộ những số n sao cho n là một số nguyên trong khoanh vùng phạm vi từ 0 đến 19 “. Một số tác giả sử dụng dấu hai chấm ” : ” thay cho thanh dọc. [ 29 ]

Tập hợp có thể xác định bằng đệ quy. Chẳng hạn tập các số tự nhiên lẻ L có thể cho như sau:

$1\in L$
Nếu $n\in L$ $n+2\in L.$

Tập hợp rỗng[sửa|sửa mã nguồn]

Tập hợp rỗng là tập hợp duy nhất không có phần tử nào. Nó được ký hiệu là ∅ hoặc

∅

{\displaystyle \emptyset }

$\emptyset$ hoặc { }[15][31] hoặc ϕ[32] (hoặc ϕ).[33]

Tập hợp đơn điểm[sửa|sửa mã nguồn]

Tập hợp đơn điểm là tập hợp có chính xác một phần tử; một tập hợp như vậy cũng có thể được gọi là một tập hợp đơn vị.[5] Bất kỳ tập hợp nào như vậy có thể được viết dưới dạng {x} , trong đó x là phần tử. Tập hợp {x} và phần tử x có nghĩa khác nhau; Halmos chỉ ra một phép tương tự rằng một chiếc hộp đựng một chiếc mũ không giống với chiếc mũ.

Tập hợp con[sửa|sửa mã nguồn]

Nếu mọi phần tử của tập A cũng có mặt trong B, thì A được mô tả là một tập con của B, hoặc được chứa trong B, được viết A ⊆ B,[35] hoặc B ⊇ A.[15][36] Kí hiệu thứ hai có thể được đọc là B chứa A, hoặc B bao gồm A. Các mối quan hệ giữa các tập hợp lập ra bởi ⊆ được gọi bao gồm hay chứa đựng. Hai tập hợp bằng nhau nếu chúng chứa nhau: A ⊆ B và B ⊆ A tương đương với A = B.[27]

Nếu A là tập con của B mà A không bằng B thì A được gọi là tập con thực sự của B. Điều này có thể được viết A ⊊ B. Tương tự như vậy, B ⊋ A có nghĩa là B là một tập hợp chứa thực sự của A, tức là B chứa A, và không bằng A.

Cặp toán tử thứ ba ⊂ và ⊃ được các tác giả khác nhau sử dụng khác nhau: một số tác giả sử dụng A ⊂ B và B ⊃ A có nghĩa là A là bất kỳ tập con nào của B (và không nhất thiết phải là tập hợp con thực sự),[38] trong khi những người khác chỉ viết A ⊂ B và B ⊃ A khi mà A là một tập hợp con thực sự của B.[35]

Sơ đồ Euler và sơ đồ Venn[sửa|sửa mã nguồn]

A là một tập hợp con của B

Sơ đồ Euler là một màn biểu diễn đồ họa của một tập hợp những tập hợp ; mỗi tập hợp được miêu tả như một vùng phẳng được một vòng tròn bao quanh, với những thành phần của nó bên trong. Nếu A là một tập con của B, thì vùng đại diện thay mặt cho A nằm trọn vẹn bên trong vùng đại diện thay mặt cho B. Nếu hai tập hợp không có thành phần nào chung thì những vùng không giao nhau .

Ngược lại, một sơ đồ Venn là một biểu diễn đồ họa của n tập hợp, trong đó n vòng chia mặt phẳng thành 2n vùng sao cho mỗi cách chọn một số trong n tập hợp (có thể là tất cả hoặc không), có một vùng cho các phần tử thuộc về tất cả các tập hợp đã chọn và không thuộc về các tập hợp khác. Ví dụ, nếu các tập hợp là A, B và C, thì phải có một vùng cho các phần tử bên trong A và C và bên ngoài B (ngay cả khi các phần tử đó không tồn tại).

Các tập hợp số đặc biệt quan trọng[sửa|sửa mã nguồn]

Có những tập hợp có tầm quan trọng toán học, mà những nhà toán học đề cập đến liên tục, đến nỗi chúng có được những cái tên đặc biệt quan trọng và những quy ước ký hiệu để xác lập chúng .

Nhiều tập hợp quan trọng này được biểu diễn trong các văn bản toán học sử dụng chữ in đậm (ví dụ:

{\displaystyle {\mathbf {Z}}}

${\mathbf {Z}}$ ) hoặc chữ viền đậm (ví dụ:

{\displaystyle \mathbb {Z} }

${\mathbb Z}$ ).[39] Chúng bao gồm[15]

Mỗi tập hợp số trên có vô số thành phần. Mỗi tập hợp là một tập hợp con của những tập hợp được liệt kê bên dưới nó .

Tập hợp các số dương hoặc âm đôi khi được biểu thị bằng dấu cộng và dấu trừ tương ứng. Ví dụ,

{\displaystyle \mathbf {Q} ^{+}}

$\mathbf {Q} ^{+}$ biểu thị tập hợp các số hữu tỉ dương.

Một hàm số (hoặc ánh xạ) từ tập hợp A đến tập hợp B là một quy tắc gán cho mỗi phần tử “đầu vào” của A một “đầu ra” là phần tử của B ; chính thức hơn, một hàm là một loại quan hệ đặc biệt, một quan hệ liên quan mỗi phần tử của A với chính xác một phần tử của B. Một hàm được gọi là

đơn ánh nếu nó ánh xạ bất kỳ hai phần tử khác nhau của A với các phần tử khác nhau của B ,
toàn ánh nếu với mọi phần tử của B, có ít nhất một phần tử của A ánh xạ tới nó, và
song ánh nếu hàm vừa là đơn ánh vừa là toàn ánh – trong trường hợp này, mỗi phần tử của A được nối với một phần tử duy nhất của B và mỗi phần tử của B được nối với một phần tử duy nhất của A, và không có phần tử chưa được ghép nối.

Các phép toán cơ bản[sửa|sửa mã nguồn]

Các định nghĩa[sửa|sửa mã nguồn]

Hợp (Union): Hợp của A và B là tập hợp gồm tất cả các phần tử thuộc ít nhất một trong hai tập hợp A và B, ký hiệu A $\cup$

Ta có A

∪ { \ displaystyle \ cup }

\in

∈ { \ displaystyle \ in }

Giao (Intersection): Giao của hai tập hợp A và B là tập hợp tất cả các phần tử vừa thuộc A, vừa thuộc B, ký hiệu A $\cap$

Ta có A

∩ { \ displaystyle \ cap }

∈ { \ displaystyle \ in }

∈ { \ displaystyle \ in }

Hiệu (Difference): Hiệu của tập hợp A với tập hợp B là tập hợp tất cả các phần tử thuộc A nhưng không thuộc B, ký hiệu $A\setminus B$

Ta có: A \ B = {x: x

∈ { \ displaystyle \ in }

\notin

Lưu ý, A \ B

\neq

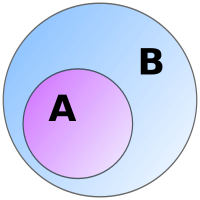Phần bù của A trong B

Phần bù (Complement): là hiệu của tập hợp con. Nếu A $\subset$ CAB (hay CB A)
Trong nhiều trường hợp, khi tất cả các tập hợp đang xét đều là tập con của một tập hợp U (được gọi là tập vũ trụ-đôi khi có nghĩa như trường hay không gian – trong vật lý; hay cũng gọi là tập phổ dụng, giống như trong đại số phổ dụng), người ta thường xét phần bù của mỗi tập A, B, C,… đang xét trong tập U, khi đó ký hiệu phần bù không cần chỉ rõ U mà ký hiệu đơn giản là CA,CB,… hoặc $\overline {A}$ $\overline {B}$

Các đặc thù cơ bản[sửa|sửa mã nguồn]

Các phép toán trên tập hợp có những đặc thù sau :

∪ { \ displaystyle \ cup }

∩ { \ displaystyle \ cap }

Phát biểu : giao hoặc hợp của một tập hợp với chính nó cho tác dụng là chính nó. Mặt khác, hợp của một tập với phần bù của nó cũng là chính nó nhưng giao của một tập với phần bù của nó lại là một tập rỗng .

Luật hấp thụ (còn gọi là luật bao hàm):

∪ { \ displaystyle \ cup }

∩ { \ displaystyle \ cap }

∩ { \ displaystyle \ cap }

∪

{\displaystyle \cup }

Xem thêm: “Không” có ý nghĩa gì?

Luật hấp thụ còn được viết dưới dạng khác như sau:

Nếu A

⊂ { \ displaystyle \ subset }

thì A

∪ { \ displaystyle \ cup }

∩ { \ displaystyle \ cap }

Luật giao hoán:

∪ { \ displaystyle \ cup }

∪ { \ displaystyle \ cup }

∩ { \ displaystyle \ cap }

∩ { \ displaystyle \ cap }

Luật kết hợp:

∩ { \ displaystyle \ cap }

∩ { \ displaystyle \ cap }

∩ { \ displaystyle \ cap }

∩ { \ displaystyle \ cap }

∪ { \ displaystyle \ cup }

∪ { \ displaystyle \ cup }

∪ { \ displaystyle \ cup }

∪ { \ displaystyle \ cup }

Luật phân phối:

∩ { \ displaystyle \ cap }

∪ { \ displaystyle \ cup }

∩ { \ displaystyle \ cap }

∪ { \ displaystyle \ cup }

∩ { \ displaystyle \ cap }

∪ { \ displaystyle \ cup }

∩ { \ displaystyle \ cap }

∪ { \ displaystyle \ cup }

∩ { \ displaystyle \ cap }

∪ { \ displaystyle \ cup }

Luật De Morgan:

\overline {A\cup B}

\overline {A}\cap \overline {B}

\overline {A\cap B}

\overline {A}\cup \overline {B}

Một tập hợp mới có thể được xây dựng bằng cách liên kết mọi phần tử của một tập hợp với mọi phần tử của một tập hợp khác. Tích Descartes của hai tập A và B, ký hiệu là A × B,[15] là tập hợp của tất cả các cặp có thứ tự (a, b) sao cho a là phần tử của A và b là phần tử của B.

Ví dụ :

{ 1, 2 } × { red, white, green } = { ( 1, red ), ( 1, white ), ( 1, green ), ( 2, red ), ( 2, white ), ( 2, green ) } .
{ 1, 2 } × { 1, 2 } = { ( 1, 1 ), ( 1, 2 ), ( 2, 1 ), ( 2, 2 ) } .
{ a, b, c } × { d, e, f } = { ( a, d ), ( a, e ), ( a, f ), ( b, d ), ( b, e ), ( b, f ), ( c, d ), ( c, e ), ( c, f ) } .

Một số đặc thù cơ bản của tích Descartes :

A × ∅ = ∅.
A × (B ∪ C) = (A × B) ∪ (A × C).
(A ∪ B) × C = (A × C) ∪ (B × C).

Cho A và B là các tập hữu hạn; thì lực lượng của tích Descartes là tích của các lực lượng:

| A × B | = | B × A | = | A | × | B |.

Khái quát hoá khái niệm số lượng phần tử của các tập hợp hữu hạn là khái niệm lực lượng của tập hợp (Cardinality).

Hai tập hợp được gọi là có cùng lực lượng nếu có một tuy nhiên ánh giữa chúng. Các tập hợp hữu hạn có cùng lực lượng khi và chỉ khi chúng có cùng số thành phần theo nghĩa thường thì .
Tập hợp A và tập hợp B có cùng lực lượngKhác biệt cơ bản của những tập hữu hạn với những tập vô hạn là mọi tập hữu hạn không có cùng lực lượng với một tập con thực sự của nó. Đối với những tập hợp vô hạn thì không phải như vậy. Sau đây là một vài ví dụ đơn thuần :

Tập con ${\mathbb N}\setminus \{0\}$ ${\mathbb N}$ ánh xạ sau là song ánh hay không:

\phi :{\mathbb N}\to {\mathbb N}\setminus \{0\}

n\longmapsto n+1

Nghĩa là chúng có cùng lực lượng .

Georg Cantor đã chứng minh rằng không thể có một song ánh giữa tập các số tự nhiên và tập hợp các số thực, vì thế lực lượng của tập hợp số tự nhiên là “nhỏ hơn” lực lượng của tập số thực. Các tập có cùng lực lượng với tập số tự nhiên được gọi là các tập đếm được, các tập hợp có cùng lực lượng với tập số thực được gọi là tập có lực lượng continuum.

|{\mathbb {Z}}|<|{\mathbb {R}}|

Nếu ký hiệu

|{\mathbb {Z}}|

\aleph _{0}

aleph-null”) và

|{\mathbb {R}}|

2^{{\aleph _{0}}}

| Z | { \ displaystyle | \ mathbb { Z } | }

2 ℵ 0 { \ displaystyle 2 ^ { \ aleph _ { 0 } } }

B(E) là tập các bộ phận của tập E.

Khi đó, P gọi là 1 phân hoạch của E ( Une Partition d’ensemble E ) nếu:

P là một bộ phận của B(E).
Với mọi tập Ai của $∈ { \ displaystyle \ in }$ i ≠ $∅ { \ displaystyle \ emptyset }$
Với mọi phần tử Ai ≠ Aj $∈ { \ displaystyle \ in }$ i $∩ { \ displaystyle \ cap }$ j = $∅ { \ displaystyle \ emptyset }$
Với mọi phần tử x $∈ { \ displaystyle \ in }$ $∈ { \ displaystyle \ in }$ i của P ta được E)

Ví dụ: E = {a,b,c}.
P={{a},{b,c}} là 1 phân hoạch của E. Vì:

P là một bộ phận của B(E) (Hiển nhiên).
Xét tất cả các phần tử của P: A1 = {a} ≠ $∅ { \ displaystyle \ emptyset }$ 2 = {b,c} ≠ $∅ { \ displaystyle \ emptyset }$
{a} $∩ { \ displaystyle \ cap }$ $∅ { \ displaystyle \ emptyset }$
{a} U {b,c} = E

Tập hợp xuất hiện khắp nơi trong toán học tân tiến. Ví dụ, những cấu trúc trong đại số trừu tượng, ví dụ điển hình như nhóm, trường và vòng, là những tập hợp được đóng dưới một hoặc nhiều phép toán .

Một trong những ứng dụng chính của lý thuyết tập hợp ngây thơ là trong việc xây dựng các quan hệ. Một mối quan hệ từ một tập xác định A đến một tập hợp đích B là một tập hợp con của tích Descartes A × B. Ví dụ, xem xét tập hợp S = {đấm, giấy, kéo} của các hình trong trò chơi oẳn tù tì, quan hệ “thắng” từ S đến S là tập hợp B = {(kéo,giấy), (giấy,đấm), (đấm,kéo)} ; do đó x thắng y trong trò chơi oẳn tù tì nếu cặp (x,y) là phần tử của B. Một ví dụ khác là tập F của tất cả các cặp (x, x2), trong đó x là số thực. Quan hệ này là một tập con của R × R, bởi vì tập hợp tất cả các bình phương là tập hợp con của tập hợp tất cả các số thực. Vì với mọi x trong R, một và chỉ một cặp (x,…) được tìm thấy trong F, nó được gọi là một hàm số. Trong ký hiệu hàm số, quan hệ này có thể được viết dưới dạng F(x) = x2.

Giả thuyết Continuum[sửa|sửa mã nguồn]

Ta đã thấy là lực lượng đếm được nhỏ hơn lực lượng Continuum. Tuy nhiên, có hay không một tập hợp có lực lượng lớn hơn lực lượng đếm được và nhỏ hơn lực lượng continuum lại là một vấn đề khác, Cantor giả thiết rằng không có điều đó (giả thiết continuum – tiếng Anh: continuum hypothesis).

\not \exists {\mathbb {A}}:\aleph _{0}<|{\mathbb {A}}|<2^{{\aleph _{0}}}.

Điều này tương tự với :

2^{{\aleph _{0}}}=\aleph _{1}

Cantor phát biểu giả thuyết Continuum năm 1878, và năm 1900 nó là bài toán tiên phong trong 23 bài toán Hilbert đưa ra. Kết luận ở đầu cuối là giả thuyết này độc lập với ZFC, tức là ta hoàn toàn có thể chứng minh và khẳng định hay phủ định giả thuyết Continuum, và thêm nó vào như một tiên đề độc lập với ZFC, theo nghĩa nếu ZFC đồng nhất thì triết lý mới cũng đồng nhất. Sự độc lập này được chứng tỏ năm 1963 bởi Paul Cohen, dựa trên những khu công trình năm 1940 của Kurt Gödel. Cohen được trao phần thưởng Fields năm 1966 cho chứng tỏ này .

Sau đó, giả thuyết Continuum vẫn tiếp tục được nghiên cứu trên những khía cạnh khác.

Xem thêm: ABO là gì? Đam Mỹ là gì? Tổng hợp các kiến thức liên quan về ABO

Tiên đề chọn, định lý bất toàn Godel và giả thuyết Continuum là vài trong số những khẳng định chắc chắn tiên phong được chứng tỏ là độc lập với ZF. Sau này, nhiều chứng minh và khẳng định khác trong giải tích, tô-pô và triết lý độ đo cũng được chứng tỏ là độc lập với ZF .

Hoàng Xuân Sính, 1972, Đại số đại cương (tái bản lần thứ tám), Nhà xuất bản giáo dục

Liên kết ngoài[sửa|sửa mã nguồn]

Source: https://dvn.com.vn
Category: Hỏi Đáp