Cho logab= 2 ; logac= 3. Tính giá trị của biểu thức logax, biết rằng x= a căn b^ 3/ c^ 2…
LÝ THUYẾT
1. Khái niệm lũy thừa
1.1 Lũy thừa với số mũ nguyên
Cho n là một số nguyên dương.
Với a là số thực tùy ý, lũy thừa bậc n của a là tích của n thừa số a.
an = a.a.a… a (n thừa số a)
Với a ≠ 0, ta có: a0 = 1 và a-n=1an.
Trong biểu thức am ; ta gọi a là cơ số, số nguyên m là số mũ.
– Chú ý:
00 và 0–n không có nghĩa.
Lũy thừa với số mũ nguyên có các tính chất tương tự của lũy thừa với số mũ nguyên dương.
Ví dụ. Tính giá trị biểu thức:
A=(12)-3. 8+ 4-2. 24+(13)-3.127
Lời giải:
A=(12)-3. 8+ 4-2. 24+(13)-3.127
A= 23. 8+(14)2. 16+ 33.127A= 8.8+116.16+ 27.127
A = 64 + 1 + 1 = 66.
1.2 Phương trình xn = b.
Đồ thị của hàm số y = x2k + 1 có dạng tương tự đồ thị hàm số y = x3 và đồ thị hàm số y = x2k có dạng tương tự đồ thị hàm số y = x4.
Từ đó, ta có kết quả biện luận số nghiệm của phương trình xn = b như sau:
a) Trường hợp n lẻ:
Với mọi số thực b, phương trình có nghiệm duy nhất.
b) Trường hợp n chẵn:
Với b < 0, phương trình vô nghiệm.
Với b = 0 , phương trình có một nghiệm x = 0.
Với b > 0, phương trình có hai nghiệm đối nhau.
1.3 Căn bậc n
a) Khái niệm: Cho số thực b và số nguyên dương n (n≥2). Số a được gọi là căn bậc n của số b nếu an = b.
Ví dụ. Căn bậc ba của 27 là 3.
Căn bậc bốn của 256 là 4 và – 4.
– Từ định nghĩa và kết quả biện luận về số nghiệm của phương trình xn = b; ta có:
Với n lẻ và b∈R: Có duy nhất một căn bậc n của b, kí hiệu là bn.
Với n chẵn và :
+ b < 0 : không tồn tại căn bậc n của b.
+ b = 0: có một căn bậc n của b là số 0.
+ b > 0: có hai căn trái dấu; kí hiệu giá trị dương là bn; còn giá trị âm là -bn.
b) Tính chất của căn bậc n
Từ định nghĩa ta có các tính chất sau:
an.bn=abnanbn=abn(an)m=amn
ann={a; khi n le|a|; khi n chan
akn=ank
Ví dụ. Rút gọn các biểu thức:
a) 93.-33;
b) (-5)44.
Lời giải:
a) 93.-33=9.(-3)3=-273=-3
b) (-5)44=|-5|= 5.
1.4 Lũy thừa với số mũ hữu tỉ.
– Cho số thực a dương và số hữu tỉ r=mn; trong đó m∈Z;n∈N;n≥2. Lũy thừa của a với số mũ r là số ar xác định bởi: ar=amn=amn.
Ví dụ.
2713=273= 3932=93= 27 .
1.5 Lũy thừa với số mũ vô tỉ.
Cho a là một số dương, α là một số vô tỉ. Ta thừa nhận rằng, luôn có một dãy số hữu tỉ (rn) có giới hạn là α và dãy số tương ứng (arn) có giới hạn không phụ thuộc vào việc chọn dãy số (rn).
– Ta gọi giới hạn của dãy số (arn) là thừa số của a với số mũ α, kí hiệu là aα.
aα=limn→+∞arnα=limn→+∞arn.
– Chú ý: Từ định nghĩa, ta có: 1α=1;(α ∈R).
2. Tính chất lũy thừa với số mũ thực.
Cho a; b là những số thực dương, α, β là những số thực tùy ý. Khi đó, ta có:
aα.aβ=aα +βaαaβ=aα -β
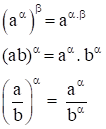
Nếu a > 1 thì aα>aβ khi và chỉ khi α > β.
Nếu a < 1 thì aα>aβ khi và chỉ khi α < β.
Ví dụ. Rút gọn biểu thức:
A=a5 + 2.a4-5(a3 -1)3 +1vớia>0
.
Lời giải:
Với a > 0 ta có:
A=a5 + 2.a4-5(a3 -1)3 +1=a5 + 2+ 4-5a(3 -1).(3 +1)=a6a2=a4.
Ví dụ. So sánh các số (23)3 + 1 và (23)2.
Lời giải:
Ta có: 3+ 1> 2 và 0<23< 1
Suy ra: (23)3 + 1< (23)2.
3. Khái niệm hàm số lũy thừa
– Hàm số y=xα, với α ∈R, được gọi là hàm số lũy thừa.
Ví dụ. Các hàm số y=x3 +1;y=1×2;y=x5;y=xπ -3 là những hàm số lũy thừa.
– Chú ý:
Tập xác định của hàm số lũy thừa y=xα tùy thuộc vào giá trị của α. Cụ thể:
+ Với α nguyên dương, tập xác định là R.
+ Với α nguyên âm hoặc bằng 0; tập xác định là R\{0}.
+ Với α không nguyên, tập xác định là (0;+∞).
4. Đạo hàm của hàm số lũy thừa
– Hàm số lũy thừa y=xα(α ∈R) có đạo hàm với mọi x > 0 và (xα)’=α.xα -1.
– Ví dụ.
a) (x25)’=25.x-35
b) (x7)’=7.x7 -1.
– Chú ý: Công thức tính đạo hàm của hàm hợp đối với hàm số lũy thừa có dạng:
(uα)’=α.uα -1.u’
– Ví dụ. Tính đạo hàm của hàm số y=(2x+23x-2)13.
Lời giải:
Ta có:
y’=13.(2x+23x-2)-23.(2x+23x-2)’=13.(2x+23x-2)-23.(4x+3).
5. Khảo sát hàm số lũy thừa y = xα
Tập xác định của hàm số lũy thừa y=xα luôn chứa khoảng (0;+∞) với α ∈R. Trong trường hợp tổng quát, ta khảo sát hàm số y=xαtrên khoảng này (gọi là tập khảo sát).
y=xα;α> 0
y=xα;α< 0
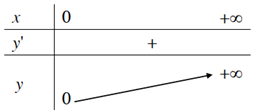
1. Tập khảo sát: (0;+∞)
2. Sự biến thiên
y’=α.xα -1> 0;∀x> 0
.
Giới hạn đặc biệt:
limx→0+xα= 0;limx→ +∞xα=+∞
Tiệm cận: Không có
3. Bảng biến thiên
4. Đồ thị (với α > 0)
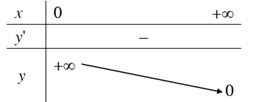
1. Tập khảo sát: (0;+∞)
2. Sự biến thiên
y’=α.xα -1< 0;∀x> 0
Giới hạn đặc biệt:
limx→0+xα=+∞;limx→+∞xα= 0
Tiệm cận:
Trục Ox là tiệm cận ngang.
Trục Oy là tiệm cận đứng của đồ thị.
3. Bảng biến thiên.
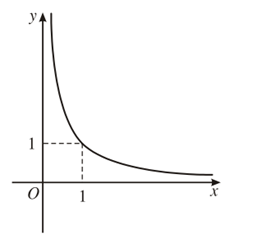
4. Đồ thị (với α < 0)
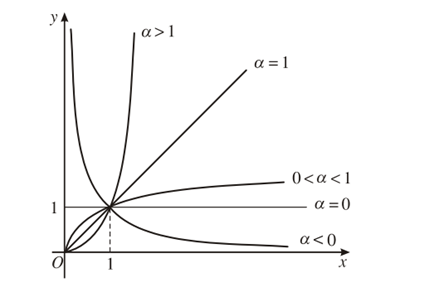
Đồ thị của hàm số lũy thừa y = xα luôn đi qua điểm (1; 1).
– Chú ý: Khi khảo sát hàm số lũy thừa với số mũ cụ thể, ta phải xét hàm số đó trên toàn bộ tập xác định của nó.
Ví dụ. Khảo sát sự biến thiên và vẽ đồ thị của hàm số y=x-25.
Lời giải:
1. Tập xác định: D=(0;+∞)
2. Sự biến thiên.
Chiều biến thiên y’=-25x-75
Ta có: y’ < 0 trên khoảng D=(0;+∞) nên hàm số đã cho nghịch biến.
Tiệm cận: limx→0+y=+∞;limx→ +∞y= 0
Đồ thị có tiệm cận ngang là trục hoành và có tiệm cận đứng là trục tung.
Bảng biến thiên
3. Đồ thị
Bảng tóm tắt các tính chất của hàm số lũy thừa y=xα trên khoảng (0;+∞).
α > 0
α< 0
Đạo hàm
y’=α.xα -1
y’=α.xα-1
Chiều biến thiên
Hàm số luôn đồng biến
Hàm số luôn nghịch biến
Tiệm cận
Không có
Tiệm cận ngang là trục Ox;
Tiệm cận đứng là trục Oy
Đồ thị
Đồ thị luôn đi qua điểm (1; 1).
6. Khái niệm về lôgarit
6.1 Định nghĩa
Cho hai số dương a; b với a ≠ 1 . Số α thỏa mãn đẳng thức aα = b được gọi là logarit cơ số a của b và kí hiệu là logab.
α=logab⇔aα=b
Ví dụ.
a) log3 27 = 3 vì 33 = 27.
b)log(116)4=-2 vì 4-2=116.
– Chú ý: Không có logarit của số âm và số 0.
6.2 Tính chất
Cho hai số dương a và b; a ≠ 1. Ta có các tính chất sau đây:
loga1 = 0; logaa = 1
alogab=b;log(aα)a=α
Ví dụ.
4-2log43=(4log43)-2= 3-2=19
log(127)3=log3(3-3)=-3
7. Quy tắc tính logarit
7.1 Logarit của một tích
– Định lí 1. Cho ba số dương a; b1 ;b2 với a ≠ 1. Ta có:
loga(b1.b)2=logab1+logab2
Logarit của một tích bằng tổng các logarit.
Ví dụ.
log212+log213=log2(12.13)=log24=2
– Chú ý:
Định lí 1 có thể mở rộng cho tích n số dương:
loga(b1.b…2.bn)=logab1+logab+2….+logabn
( a; b1; b2; ..; bn > 0; a ≠ 1)






