Top 8 am-gm inequality in 2023
Below are the best information and knowledge on the subject am-gm inequality compiled and compiled by our own team dvn:
Mục Lục
1. Art of Problem Solving
Author: en.wikipedia.org
Date Submitted: 01/15/2022 06:05 AM
Average star voting: 3 ⭐ ( 50720 reviews)
Summary:
Match with the search results: Thus the AM–GM inequality states that only the n-cube has the smallest sum of lengths of edges connected to each vertex amongst all n-dimensional boxes with ……. read more
![]()
2. Arithmetic Mean – Geometric Mean | Brilliant Math & Science Wiki
Author: artofproblemsolving.com
Date Submitted: 12/03/2019 05:53 PM
Average star voting: 4 ⭐ ( 45402 reviews)
Summary: The arithmetic mean-geometric mean (AM-GM) inequality states that the arithmetic mean of non-negative real numbers is greater than or equal to the geometric mean of the same list. Further, equality holds if and only if every number in the list is the same. Mathematically, for a collection of …
Match with the search results: In mathematics, the inequality of arithmetic and geometric means, or more briefly the AM–GM inequality, states that the arithmetic mean of a list of non-negative real numbers is greater than or equal ……. read more

3. AM GM Inequality Solved Problems
Author: brilliant.org
Date Submitted: 10/29/2022 05:29 PM
Average star voting: 5 ⭐ ( 69579 reviews)
Summary: Inequality of arithmetic and geometric mean is one of the fundamental inequalities in Algebra. Learn easy way of AM-GM Concept used in many inequality examples.
Match with the search results: The AM-GM Inequality is among the most famous inequalities in algebra and has cemented itself as ubiquitous across almost all competitions. Applications exist ……. read more

4. Proofs of AM-GM inequality
Author: byjus.com
Date Submitted: 09/15/2021 12:19 AM
Average star voting: 5 ⭐ ( 75308 reviews)
Summary:
Match with the search results: The arithmetic mean-geometric mean (AM-GM) inequality states that the arithmetic mean of non-negative real numbers is greater than or equal to the geometric ……. read more
5. AM-GM Inequality
Author: amsi.org.au
Date Submitted: 07/17/2021 08:27 PM
Average star voting: 4 ⭐ ( 30376 reviews)
Summary:
Match with the search results: The AM–GM inequality, or inequality of arithmetic and geometric means, states that the arithmetic means of a list of non-negative real numbers is greater than ……. read more
![]()
6. The Arithmetic-Geometric Mean Inequality
Author: math.stackexchange.com
Date Submitted: 01/12/2021 02:33 AM
Average star voting: 4 ⭐ ( 73689 reviews)
Summary: Suppose that x and y are non-negative real numbers, not necessarily distinct. The famous arithmetic-geometric mean inequality says that: Again with equality if and only if all of the numbers are…
Match with the search results: The AM–GM inequality … Exercise 11 gave a geometric proof that the arithmetic mean of two positive numbers a and b is greater than or equal to their geometric ……. read more
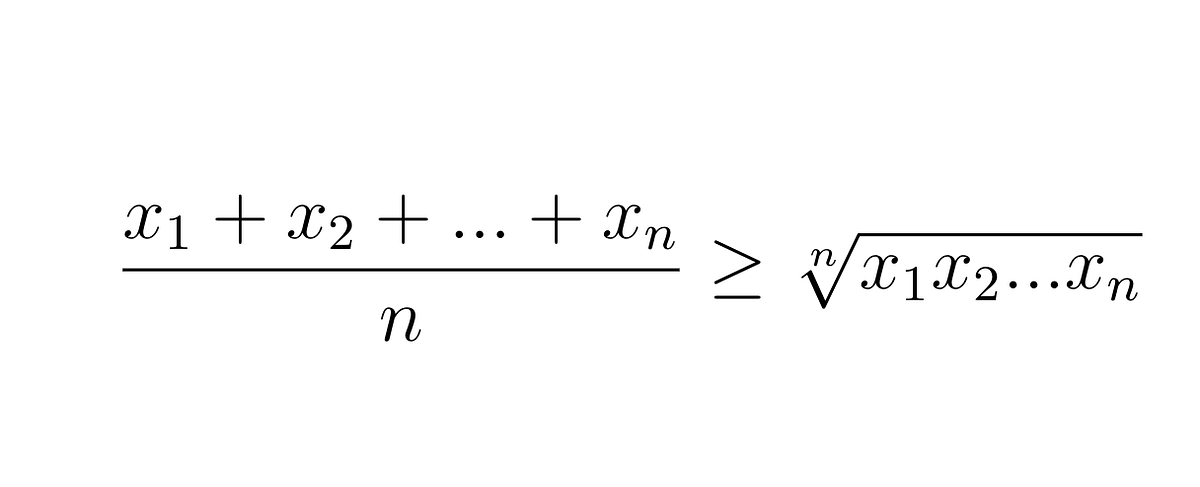
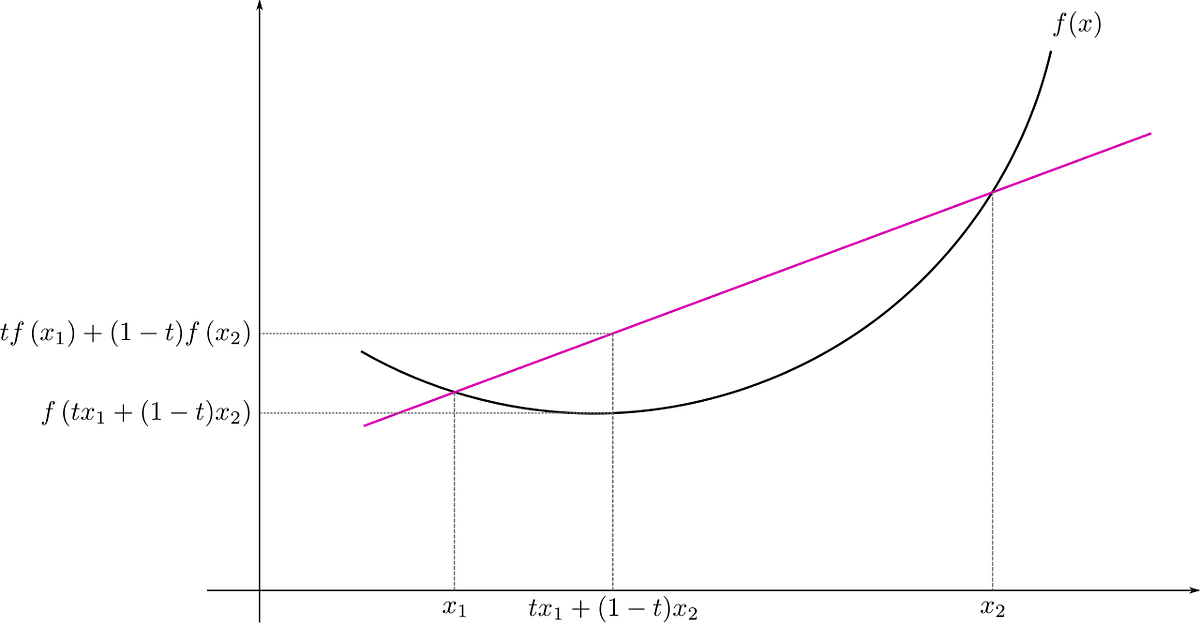
7. Convexity and Jensen’s Inequality (and the AM-GM Inequality)
Author: web.williams.edu
Date Submitted: 09/06/2020 09:55 AM
Average star voting: 5 ⭐ ( 50539 reviews)
Summary: In this (relatively) short article, we will discuss the extremely useful Jensen’s inequality, named after the Danish mathematician Johan Jensen. Jensen’s inequality can be viewed as a generalization…
Match with the search results: AM-GM inequality says that for any a1,…,an>0, we have a1+⋯+ann≥n√a1⋯an with equality holding if and only if a1=⋯=an. Here is Cauchy’s ……. read more
8. 4.2: Arithmetic and Geometric Means
Author: mathcircle.berkeley.edu
Date Submitted: 07/08/2021 10:17 AM
Average star voting: 5 ⭐ ( 30700 reviews)
Summary:
Match with the search results: √a1 ···an. (1.2). Theorem 1.3 (Arithmetic Mean – Geometric Mean). Let a1,…,an be n positive numbers. Then. AM(a1,…,n ) ≥ GM(a1,…,an)….. read more







