Đề kiểm tra 45 phút (1 tiết) – Đề số 3 – Chương 1 – Hình học 7>

Đề bài

Bài 1. Cho hình vẽ, biết \(\widehat {{B_3}} = {80^o}\).

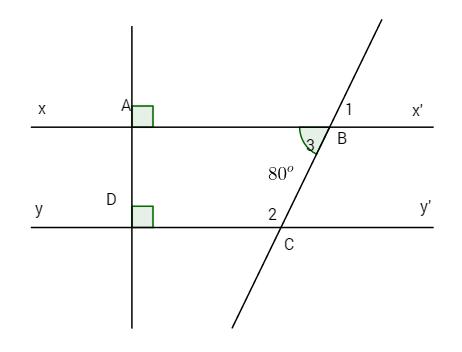
a ) Tính số đo góc \ ( \ widehat { { B_1 } } \ ) và \ ( \ widehat { { C_2 } } \ ) .
b ) Vẽ tia phân giác Ct của \ ( \ widehat { BCy ‘ } \ ), tia Ct cắt xx ’ ở E. So sánh \ ( \ widehat { BCE } \ ) và \ ( \ widehat { BEC } \ ) .
c ) Vẽ tia phân giác Bz của \ ( \ widehat { ABC } \ ), vì sao Bz / / EC ?

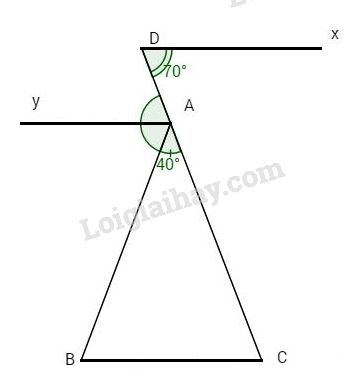
Bài 2. Cho có \(\widehat A = {40^o}\). Trên tia đối của tia AC lấy điểm D. Trên nửa mặt phẳng bờ AC không chứa điểm B vẽ tia Dx//BC. Biết \(\widehat {xDC} = {70^o}\).

a ) Tính số đo góc \ ( \ widehat { ACB } \ ) .
b ) Vẽ tia Ay là tia phân giác của \ ( \ widehat { BAD } \ ). Chứng minh Ay / / BC .

Bài 3. Cho đoạn thẳng MN. Từ một điểm P nằm ngoài đoạn thẳng MN, vẽ PH vuông góc với MN (H thuộc MN) và Px//MN.

a ) Px và PH có vuông góc với nhau không ? Tại sao ?
b ) Vẽ trung trực d của đoạn NM, em có nhận xét gì về đường thẳng d và đường thẳng PH. Hãy lý giải nhận xét đó .

Bài 4. Cho hình vẽ.

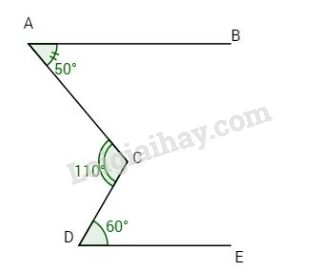
Chứng tỏ AB / / DE .

Phương pháp giải:

+ Nếu 1 đường thẳng cắt hai đường thẳng song song thì :
a ) Các cặp góc so le trong bằng nhau .
b ) Các cặp góc đồng vị bằng nhau .
c ) Các cặp góc trong cùng phía bù nhau
+ \ ( \ left \ { \ matrix { a \ bot c \ hfill \ cr b \ bot c \ hfill \ cr } \ right. \ Rightarrow a / / b \ )
+ \ ( \ left \ { { \ begin { array } { * { 20 } { c } } { a \ bot b } \ \ { b / / c } \ end { array } } \ right. \ Rightarrow a \ bot c \ )
+ \ ( \ left \ { { \ begin { array } { * { 20 } { c } } { a / / b } \ \ { b / / c } \ end { array } } \ right. \ Rightarrow a / / c \ )
+ Tính chất tia phân giác của 1 góc

LG bài 1

Lời giải chi tiết:

Bài 1.

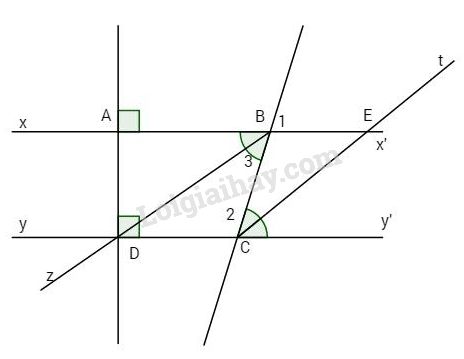
a ) \ ( \ widehat { { B_1 } } = \ widehat { { B_3 } } = { 80 ^ o } \ ) ( đối đỉnh )
Ta có \ ( \ left \ { \ matrix { xx ‘ \ bot AD \ hfill \ cr yy ‘ \ bot AD \ hfill \ cr } \ right. \ Rightarrow xx ‘ / / yy ‘ \ )
( hai đường thẳng phân biệt cùng vuông góc với đường thứ ba thì chúng song song với nhau )

\( \Rightarrow \widehat {{C_2}} + \widehat {{B_3}} = {180^o}\)(cặp góc trong cùng phía)

\ ( \ Rightarrow \ widehat { { C_2 } } = { 180 ^ o } – \ widehat { { B_3 } } = { 180 ^ o } – { 80 ^ o } = { 100 ^ o }. \ )
b ) Ct là tia phân giác của góc \ ( \ widehat { BCy ‘ } \ ). Ta có \ ( \ widehat { BCE } = \ widehat { ECy ‘ } = { 1 \ over 2 } \ widehat { BCy ‘ }. \ )
lại có xx ’ / / yy ’ \ ( \ Rightarrow \ widehat { BCE } = \ widehat { ECy ‘ } \ ) ( cặp góc so le trong ) .
Do đó \ ( \ widehat { BCE } = \ widehat { BEC }. \ )
c ) Bz là tia phân giác của góc \ ( \ widehat { ABC } \ ). Ta có \ ( \ widehat { zBC } = { 1 \ over 2 } \ widehat { ABC }. \ )
Ct là tia phân giác của góc \ ( \ widehat { BCy ‘ } \ ). Ta có \ ( \ widehat { BCE } = { 1 \ over 2 } \ widehat { BCy ‘ }. \ )
Lại có xx ’ / / yy ’ \ ( \ Rightarrow \ widehat { ABC } = \ widehat { BCy ‘ } \ ) ( cặp góc so le trong ) .
Suy ra \ ( \ widehat { BCE } = \ widehat { zBC } \ ), mà 2 góc ở vị trí so le trong
\ ( \ Rightarrow AB / / DE \ )

LG bài 2

Lời giải chi tiết:

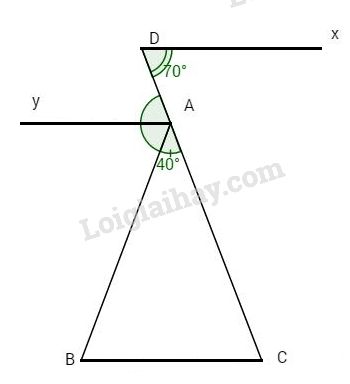
a ) Dx / / BC, hai góc \ ( \ widehat { ACB } \ ) và \ ( \ widehat { xDC } \ ) ở vị trí so le trong nên xx ’ / / yy ’ \ ( \ Rightarrow \ widehat { BCy ‘ } = \ widehat { ABC } \ Rightarrow { { \ widehat { BCy ‘ } } \ over 2 } = { { \ widehat { ABC } } \ over 2 } \ ) hay \ ( \ widehat { zBC } = \ widehat { BCE } \ ), hai góc này ở vị trí so le trong \ ( \ Rightarrow Bz / / CE. \ )
\ ( \ Rightarrow \ widehat { ACB } = \ widehat { xDC } = { 70 ^ o }. \ )
b ) Ta có \ ( \ widehat { DAB } = { 180 ^ o } – \ widehat { BAC } = { 140 ^ o } \ )
Ay là phân giác của góc \ ( \ widehat { DAB } \ )
Nên \ ( \ widehat { DAy } = \ widehat { BAy } = { { \ widehat { DAB } } \ over 2 } = { { { { 140 } ^ o } } \ over 2 } = { 70 ^ o }. \ )
Hai góc \ ( \ widehat { DAy } \ ) và \ ( \ widehat { ACB } \ ) ở vị trí đồng vị, mà \ ( \ widehat { DAy } = \ widehat { ACB } = { 70 ^ o }. \ )

LG bài 3

Lời giải chi tiết:

Bài 3.

a ) Ta có \ ( \ left \ { \ matrix { PH \ bot MN \ hfill \ cr Px / / MN \ hfill \ cr } \ right. \ Rightarrow Px \ bot PH \ )
( một đường thẳng vuông góc với một trong hai đường song song thì nó vuông góc với đường còn lại ) .
b ) d là trung trực của đoạn NM nên \ ( d \ bot NM \ ), mà \ ( PH \ bot NM \ Rightarrow d / / PH \ ) ( hai đường thẳng phân biệt cùng vuông góc với đường thứ ba thì chúng song song ) .

LG bài 4

Lời giải chi tiết:

Kẻ qua C tia Ct / / AB ( 1 ) ( tia Ct nằm trong góc \ ( \ widehat { ACD } \ ), ta có \ ( \ widehat { ACt } = \ widehat { BAC } = { 50 ^ o } \ ) ( cặp góc so le trong ) .
Tia Ct nằm giữa hai tia CD và CA, ta có \ ( \ widehat { ACt } + \ widehat { DCt } = \ widehat { ACD } \ )

\(\widehat {DCt} = \widehat {ACD} – \widehat {ACt} = {110^o} – {50^o} = {60^o}\). Hai góc \(\widehat {tDC}\) và \(\widehat {DCE}\) ở vị trí so le trong, mà \(\widehat {DCt} = \widehat {CDE} = {60^o}\) nên Ct // DE (2).

Từ ( 1 ) và ( 2 ) \ ( \ Rightarrow AB / / DE \ ) ( hai đường thẳng phân bietj cùng song song với đường thẳng thứ ba ) .

 Loigiaihay.com

Source: https://dvn.com.vn
Category: Hỏi Đáp