Các phép toán cơ bản của tập hợp và một số ví dụ minh họa
Mục Lục
Các phép toán cơ bản của tập hợp và một số ví dụ minh họa
Tập hợp là một trong những khái niệm nền tảng nhất của toán học. Nhắc đến toán là nhắc đến những phép tính thân quen, vậy tập hợp có những phép tính nào không, mời những bạn cùng tìm hiểu và khám phá .
Các phép toán cơ bản của tập hợp bao gồm hợp, giao, hiệu và phần bù. Dưới đây là mô tả của mỗi phép toán cùng với ví dụ minh họa:
- Hợp (Union):
- Phép toán hợp của hai tập hợp A và B (ký hiệu là A ∪ B) tạo ra một tập hợp mới chứa tất cả các phần tử thuộc A hoặc B hoặc cả hai.
- Ví dụ: Cho A = {1, 2, 3} và B = {3, 4, 5}. Hợp của A và B là A ∪ B = {1, 2, 3, 4, 5}.
- Giao (Intersection):
- Phép toán giao của hai tập hợp A và B (ký hiệu là A ∩ B) tạo ra một tập hợp mới chứa tất cả các phần tử thuộc cả A và B.
- Ví dụ: Cho A = {1, 2, 3} và B = {3, 4, 5}. Giao của A và B là A ∩ B = {3}.
- Hiệu (Difference):
- Phép toán hiệu của hai tập hợp A và B (ký hiệu là A \ B) tạo ra một tập hợp mới chứa tất cả các phần tử thuộc A mà không thuộc B.
- Ví dụ: Cho A = {1, 2, 3} và B = {3, 4, 5}. Hiệu của A và B là A \ B = {1, 2}.
- Phần bù (Complement):
- Phép toán phần bù của tập hợp A đối với tập hợp U (ký hiệu là A’) tạo ra một tập hợp mới chứa tất cả các phần tử không thuộc A mà thuộc U.
- Ví dụ: Cho U là tập hợp số tự nhiên từ 1 đến 10 (U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}) và A = {2, 4, 6, 8, 10}. Phần bù của A đối với U là A’ = {1, 3, 5, 7, 9}.
Các phép toán này giúp bạn xác định mối quan hệ giữa các tập hợp và thực hiện các thao tác tập hợp cơ bản. Ngoài ra, chúng còn có ứng dụng rất nhiều trong toán học và khoa học máy tính.
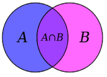
Phép giao:
Tập hợp C gồm những thành phần vừa thuộc A vừa thuộc B gọi là giao của A và B .
Kí hiệu :
C=A∩B
A ∩ B = xx ∈ A và x ∈ Bx ∈ A = x ∈ Ax ∈ B
Phép giao (nguồn: internet)
Phép hợp:
Tập hợp C gồm những thành phần thuộc A hoặc thuộc B được gọi là hợp của A và B .
Kí hiệu :
C = A ∪ B
A ∪ B = xx ∈ A hoặc x ∈ Bx ∈ A ∪ B ⇔ x ∈ A hoặc x ∈ B
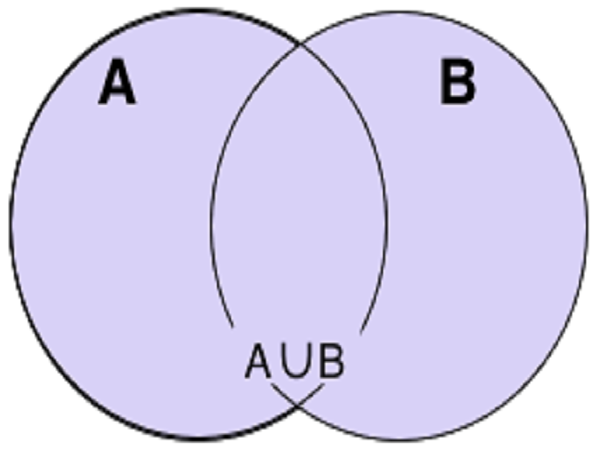
Phép hợp (nguồn: internet)
Phép hiệu:
Tập hợp C gồm những thành phần thuộc A nhưng không thuộc B được gọi là hiệu của A và B .
Kí hiệu :
C = A \ B
A \ B =xx∈A và x∉Bx∈A \ B=x∈Ax∉B
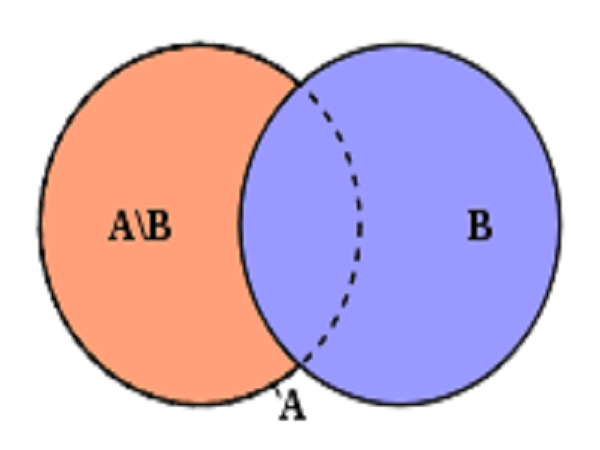
Phép hiệu ( nguồn : internet )
Phép bù:
Khi B nằm trong A ( ký hiệu B ⊂ A ) thì phần A \ B được gọi là phần bù của B trong A
Kí hiệu :
CAB = A \ B
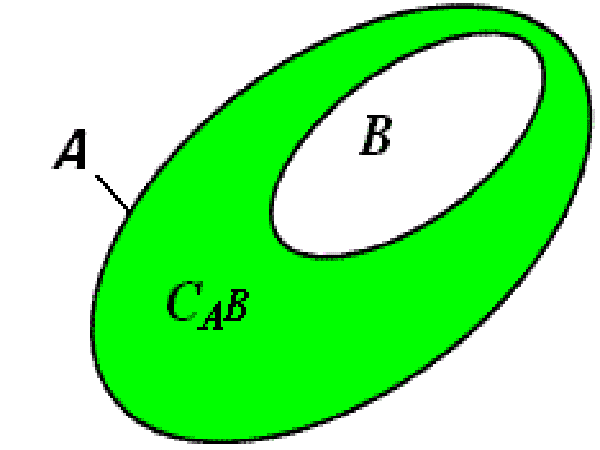
Phép bù(nguồn: internet)
Bài tập:
Ví dụ 1:
Cho 2 tập hợp A=1;2;3;4;7;9B=5;6;7;8;9
Hãy tìm A∩BA∪BA \ B
Đáp án:
A ∩ B = 7 ; 9A ∪ B = 1 ; 2 ; 3 ; 4 ; 5 ; 6 ; 7 ; 8 ; 9A \ B = 1 ; 2 ; 3 ; 4
Ví dụ 2:
Cho tập hợp A=1;2;3;4;6;8B=2;3;5C=1;3;4;8
Tìm phần bù của B trong A : CAB và phần bù của C trong A : CAC
Đáp án:
Vì B⊄A ⇔không tồn tại CAB
Xem thêm: API là gì? 4 đặc điểm nổi bật của API
Vì C ⊂ B ⇔ CAC = A \ C = 2 ; 6
Diện tích hình thoi và những lưu ý giúp bạn học Toán hiệu quả🙁 VOH ) – Trong Toán học, việc phân biệt và sử dụng công thức tính hình diện tích hình thoi là rất cần thiết. Bạn đọc hãy cùng khám phá chi tiết qua bài viết dưới đây: ( VOH ) – Trong Toán học, việc phân biệt và sử dụng công thức tính hình diện tích quy hoạnh hình thoi là rất thiết yếu. Bạn đọc hãy cùng tò mò chi tiết cụ thể qua bài viết dưới đâyNhững công thức tổ hợp xác suất cơ bản:Trong Toán học, tổ hợp là cách chọn những phần tử từ một nhóm lớn hơn mà không phân biệt thứ tự. Trong những trường hợp nhỏ hơn có thể đếm được số tổ hợp.: Trong Toán học, tổng hợp là cách chọn những thành phần từ một nhóm lớn hơn mà không phân biệt thứ tự. Trong những trường hợp nhỏ hơn hoàn toàn có thể đếm được số tổng hợp .
Source: https://dvn.com.vn
Category: Hỏi Đáp