Công suất tiêu thụ trong mạch điện không phân nhánh RLrC
Công thức tính công suất, ví dụ có lời giải chi tiết và bài tập vận dụng về công suất, hệ số công suất được trình bày rất chi tiết và tỉ mỉ trong bài viết này. Đặc biệt các trường hợp hay mắc phải sai lầm khi giải bài toán cũng đã được liệt kê.
CÔNG SUẤT TIÊU THỤ TRONG MẠCH ĐIỆNKHÔNG PHÂN NHÁNH RLrC
(Cuộn dây không thuần cảm có r).
Bạn đang đọc: Công suất tiêu thụ trong mạch điện không phân nhánh RLrC
I.Công suất tiêu thụ trong mạch RrLC không phân nhánh (cuộn dây có L,r):
+ Công suất tiêu thụ của cả đọan mạch xoay chiều : P = UIcosφ hayP. = I2 ( R + r ) = \ ( \ frac { U ^ { 2 } ( R + r ) } { Z ^ { 2 } } \ ) .+ Hệ số công suất của cả đọan mạch : \ ( cos \ varphi = \ frac { R + r } { Z } \ ) .+ Công suất tiêu thụ trên điện trở R : PR = I2. R = \ ( \ frac { U ^ { 2 } R } { Z ^ { 2 } } \ )Với Z = \ ( \ sqrt { ( R + r ) ^ { 2 } + ( Z_ { L } – Z_ { C } ) ^ { 2 } } \ )+ Công suất tiêu thụ của cuộn dây : Pr = I2. r = \ ( \ frac { U ^ { 2 }. r } { Z ^ { 2 } } \ )
+ Hệ số công suất của đọan mạch chứa cuộn dây :\(cos \varphi _{d} = \frac{r}{Z_{d}}=\frac{r}{\sqrt{r^{2}+{Z_{L}}^{2}}}\)
(Hay mạch có RLC cuộn dây có điện trở trong r (R, L, r, C)
Ví dụ 1: Một đoạn mạch điện xoay chiều gồm một cuộn dây có điện trở thuần r =20Ω và độ tự cảm L=\(\frac{0,8}{\pi }\) H, tụ điện C= \(\frac{10^{-4}}{2\pi }\)F và điện trở thuần R thay đổi được mắc nối tiếp. Điện áp hai đầu đoạn mạch ổn định. Để mạch tiêu thụ công suất cực đại thì R phải có giá trị nào sau đây?
A. 100 Ω. B. 120 Ω. C. 60 Ω. D. 80 Ω .
HD: Tính ZL= 80Ω, ZC= 200Ω, theo (17) => R=|ZL- ZC| – r = 100Ω.
Chọn A.
Ví dụ 2: Một đoạn mạch điện xoay chiều gồm một cuộn dây có điện trở thuần r =30Ω và độ tự cảm L= \(\frac{0,8}{\pi }\) H, tụ điện C= \(\frac{10^{-3}}{4\pi }\) F và điện trở thuần R thay đổi được mắc nối tiếp. Điện áp hai đầu đoạn mạch ổn định. Để công suất tiêu thụ trên R cực đại thì R phải có giá trị nào sau đây?
A. 100 W. B. 120 W. C. 50 W. D. 80 W.
HD: ZL= 80Ω, ZC= 40Ω, theo (17): R2= r2+(ZL- ZC)2 =2500 => R=50 Ω .
Chọn C
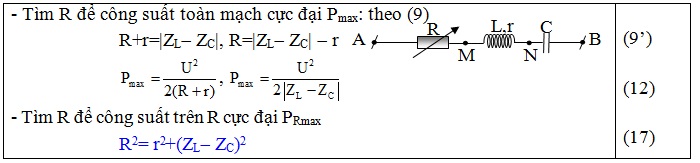
II. Công suất tiêu thụ cực đại của cả đọan mạch R thay đổi : (L,r,C, ω không đổi )
R thay đổi để Pmax: Khi L,C, ω không đổi thì mối liên hệ giữa ZL và ZC không thay đổi nên sự thay
đổi của R không gây ra hiện tượng cộng hưởng
Ta có P = ( R + r ) I2 = ( R + r ) \ ( \ frac { U ^ { 2 } } { ( R + r ) ^ { 2 } + ( Z_ { L } – Z_ { C } ) ^ { 2 } } \ )P. = \ ( \ frac { U ^ { 2 } } { ( R + r ) + \ frac { ( Z_ { L } – Z_ { C } ) ^ { 2 } } { ( R + r ) } } \ ), để P = Pmax
=> (\((R+r)+\frac{(Z_{L}-Z_{C})^{2}}{(R+r)}\)) min thì : (R+r) = |ZL- ZC|
Hay: R =|ZL- ZC| -r Công suất tiêu thụ cực đại trên (R+r): Pmax = \(\frac{U^{2}}{2\left | Z_{L}-Z_{C} \right |}\)
III. Công suất tiêu thụ cực đại trên R:
Ta có
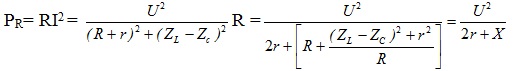
Để PR:PRmax ta phải có X = (\(R+\frac{(Z_{L}-Z_{C})^{2}+r^{2}}{R}\)) đạt giá trị min
=> \(R=\frac{(Z_{L}-Z_{C})^{2}+r^{2}}{R}\Rightarrow R=\sqrt{(Z_{L}-Z_{C})^{2}+r^{2}}\)
Lúc đó PRmax = \ ( \ frac { U ^ { 2 } } { 2 r + 2 \ sqrt { ( Z_ { L } – Z_ { C } ) ^ { 2 } + r ^ { 2 } } } \ )
Lưu ý: Có khi kí hiệu r thay bằng R0 .
+Ví dụ 3: Một biến trở R mắc nối tiếp với cuộn dây có điện trở thuần R0 = 15 Ω và độ tự cảm L = \(\frac{1}{5\pi }\) H như hình vẽ. Biết điện áp hai đầu đoạn mạch là uAB= 40\(\sqrt{2}\)cos100πt (V). Công suất toả nhiệt trên biến trở có thể đạt giá trị cực đại là bao nhiêu khi ta dịch chuyển con chạy của biến trở? Tính giá trị của biến trở lúc đó và Công suất cực đại đó?
Giải:
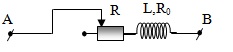
Cảm kháng : ZL = ωL = 20 Ω; U = 40 V
Công suất toả nhiệt trên R :
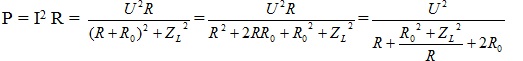
– Để Pmax thì \ ( R + \ frac { { R_ { 0 } } ^ { 2 } + { Z_ { L } } ^ { 2 } } { R } \ ) min. Vì 2R0 là 1 số ít không đổi => \ ( R = \ frac { { R_ { 0 } } ^ { 2 } + { Z_ { L } } ^ { 2 } } { R } \ )
hay R =\(\sqrt{{R_{0}}^{2}+{Z_{L}}^{2}}\)= 25 Ω và Pmax = \(\frac{U^{2}}{2(R+R_{0})}\)=20W
+Ví dụ 4: Cho đoạn mạch điện gồm diện trở R= 40Ω mắc nối tiếp với cuộn dây có điện trở hoạt động bằng 10 và tụ điện có điện dung C. Đặt vào 2 đầu đoạn mạch một điện áp u=110\(\sqrt{2}\) cos ωt, thì điện áp giữa 2 bản tụ điện lệch pha 90o so với u. Tính công suất tiêu thụ của toàn mạch .Tính công suất tiêu thụ của cuộn dây?
Giải: Lý thuyết cho ta điện áp giữa 2 bản tụ điện lệch pha 90o so với i. Mà theo đề thì điện áp giữa 2 bản tụ điện lệch pha 90o so với u nên trong mạch xảy ra cộng hưởng do đó :
\ ( I_ { max } = \ frac { U } { R + r } = \ frac { 110 } { 40 + 10 } = 2,2 A \ )Công suất toàn mạch : \ ( P_ { max } = \ frac { U ^ { 2 } } { R + r } \ ). Thế số : \ ( P_ { max } = \ frac { 110 ^ { 2 } } { 40 + 10 } = 242W \ )Công suất tiêu thụ của cuộn dây : \ ( P_ { d } = rI ^ { 2 } = 10.2,2 ^ { 2 } = 48,4 W \ ) .
IV. TRẮC NGHIỆM
Câu 1: Mạch điện xoay chiều gồm biến trở R, cuộn dây và tụ điện mắc nối tiếp. Biết cuộn dây có điện trở thuần r = 30Ω, độ tự cảm L =\(\frac{0,6}{\pi }H\) , tụ điện có điện dung C = \(\frac{1}{2\pi }\) mF. Đặt vào hai đầu đoạn mạch một điện áp xoay chiều 220V – 50Hz. Để công suất tiêu thụ trên biến trở đạt cực đại thì giá trị của biến trở phải bằng
A. 0 B. 10 C. 40. D. 50 .HD : Công suất trên biến trở cực lớn khi \ ( R = \ sqrt { r ^ { 2 } + ( Z_ { L } – Z_ { C } ) ^ { 2 } } \ ) Thế số : \ ( R = \ sqrt { 30 ^ { 2 } + ( 60-20 ) ^ { 2 } } = 50 \ Omega \ )
Chọn D.
Câu 2: Một đoạn mạch nối tiếp gồm cuộn dây có điện trở thuần r = 100\(\sqrt{3}\Omega\) và độ tự cảm L = 0,191 H, tụ điện có điện dung C = 1/4π(mF), điện trở R có giá trị thay đổi được. Điện áp đặt vào hai đầu đoạn mạch u = 200\(\sqrt{2}\)cos(100πt) V. Thay đổi giá trị của R để công suất tiêu thụ trong mạch đạt cực đại. Xác định giá trị cực đại của công suất trong mạch.
A. 200 W B. 228W C. 100W D. 50W
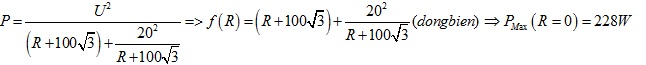
Chọn B
TÓM TẮT CÁC CÔNG THỨC VỀ CÔNG SUẤT

Tất cả nội dung bài viết. Các em hãy xem thêm và tải file chi tiết dưới đây:
Luyện Bài tập trắc nghiệm môn Vật lý lớp 12 – Xem ngay
Source: https://dvn.com.vn
Category: Tiêu Dùng






