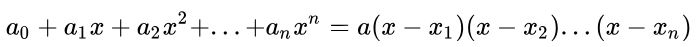Định Lý Viet (Viète) hay Hệ Thức Viet và ứng dụng của chúng
Mục Lục
1. Tìm hiểu về định lý Viet (Hệ thức vi-et)
1.1. Khái niệm:
Định lý Viet là công thức thể hiện mối quan hệ giữa các nghiệm của phương trình đa thức trong trường số phức và các hệ số do nhà toán học Pháp François Viète tìm ra. Viète được phiên âm theo tiếng Việt là Vi-ét.
Định lý Vi-et học ở chương trình đại số ở cấp 2 và cấp 3 có nội dung kỹ năng và kiến thức quan trọng so với học viên.
1.2. Định lý Vi-et thuận:
 Định lý viet thuận
Định lý viet thuận
1.3. Định lý Vi-et đảo:

1.4. Ứng dụng của hệ thức Vi-et
Theo hệ thức Vi-et, phương trình \(ax^2 + bx + c = 0\) (2) với a≠0 có hai nghiệm là x1, x2 khi và chỉ khi thỏa mãi các hệ thức:
\ ( x_1 + x_2 = \ frac { – b } { a } \ )
và
\ ( x_1 * x_2 = \ frac { c } { a } \ ) Từ hệ thức viet tất cả chúng ta hoàn toàn có thể vận dụng để tìm 2 số a và b khi biết a + b = S và a. b = P, khi đó ta chỉ cần giải phương trình \ ( x ^ 2 – Sx + P = 0 \ ), a và b chính là 2 nghiệm của phương trình. Do đó, những ứng dụng của Định lý Vi-et gồm có :
• Tính nhẩm nghiệm phương trình bậc 2. Ví dụ: Với phương trình \(x^2 – 5x + 6 = 0\), ta có thể tính nhẩm nghiệm số nguyên của phương trình là 2 và 3 bởi 2 + 3 = 5 và 2 x 3 = 6.
• Tìm 2 số khi biết tích và tổng : Nếu tổng là S, tích là P thì hai số có 2 nghiệm phương trình gồm : \ ( x ^ 2 – Sx + P = 0 \ ) ( Lưu ý, hai số trên sống sót với điều kiện kèm theo là \ ( S ^ 2 – 4P > = 0 \ ) ) • Tính giá trị những biểu thức đối xứng của 2 nghiệm phương trình bậc 2 : • Biến tam thức bậc 2 thành nhân tử : Nếu x1, x2 là nghiệm của đa thức \ ( f ( x ) = ax ^ 2 + bx + c \ ) hoàn toàn có thể nghiên cứu và phân tích thành nhân tử f ( x ) = a ( x – x1 ) ( x – x2 )
Xem thêm: Bảng công thức đạo hàm tổng hợp kèm bài tập ví dụ
2. Định lý viet bậc 2 và bậc 3
2.1. Định lý viet bậc 2
Công thức Vi-ét bộc lộ theo phương trình bậc 2 có dạng như sau nếu 2 nghiệm của phương trình lần lượt là x1 và x2, ta có công thức : \ ( ax ^ 2 + bx + c = 0 \ ), điều kiện kèm theo a # 0 thì ta có x1 + x2 = S = – b / a và x1. x2 = P = c / a
Xem thêm: Toàn bộ chi tiết về công thức LOGARIT cần biết
2.2. Định lý viet bậc 3
Phương trình \ ( ax ^ 3 + bx ^ 2 + cx + d = 0 \ ) có 3 nghiệm phân biệt x1, x2, x3 khi đó : 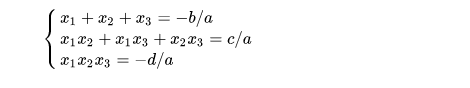 Định lý viet bậc 3
Định lý viet bậc 3
Lưu ý: Áp dụng Định lý viet bậc 3 giúp giải một số bài phương trình bậc 3 dễ dạng hơn
3. Phương trình đa thức bất kỳ
Phương trình đa thức bất kỳ có dạng:
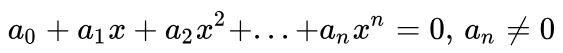
Cho x1, x2, x3,…, xn là n nghiệm của phương trình đa thức ở trên, ta có công thức như sau:
Do đó, công thức Vi-ét sẽ là tác dụng của phép tính ở vế phải và ta được : 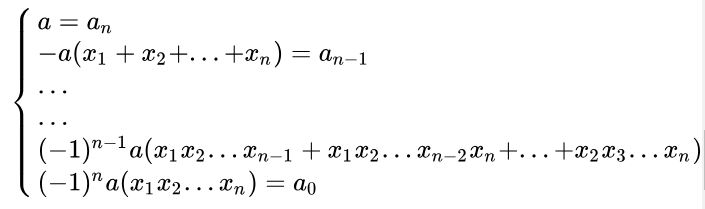

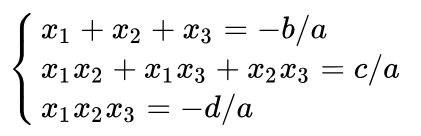
4. Các ứng dụng của định lý Vi-ét
4.1. Tìm Số Biết Tổng Và Tích Của Chúng

.JPG)


4.2. Tính giá trị các biểu thức đối xứng giữa các nghiệm
.JPG)
.JPG)




4.3. Tìm Hệ Thức Liên Hệ Giữa Các Nghiệm Phụ Thuộc Tham Số
.JPG)

.JPG)

.JPG)



4.4. Tìm Điều Kiện Của Tham Số Để 2 Nghiệm Liên Hệ Với Nhau Bởi 1 Hệ Thức Cho Trước (Điều Kiện Cho Trước)


.JPG)
.JPG)

.JPG)


4.5. Thiết Lập Phương Trình Bậc 2
Dựa trên cơ sở của định lý Vi-et, ta thiết lập phương trình bậc 2 có nghiệm là x1, x2. Nếu x1 + x2 = S ; x1. x2 = P thì nghiệm của phương trình là x1, x2 Xét những ví dụ : .JPG)



4.6. Xét Dấu Các Nghiệm





5. Bài tập ứng dụng định lý Vi-et
Sau đây là những bài tập vận dụng định lý Vi-et đã học ở trên mà tất cả chúng ta cùng tìm hiểu thêm sau đây.
Bài tập 1: Gọi các nghiệm của phương trình \(x^2 – 3x + 1 = 0\) là x1, x2. Yêu cầu tìm giá trị của các biểu thức mà không giải phương trình.

Bài giải: Có Δ = -3^2 – 4.1 = 9 – 4 = 5 > 0 => phương trình có nghiệm x1, x2 # 0
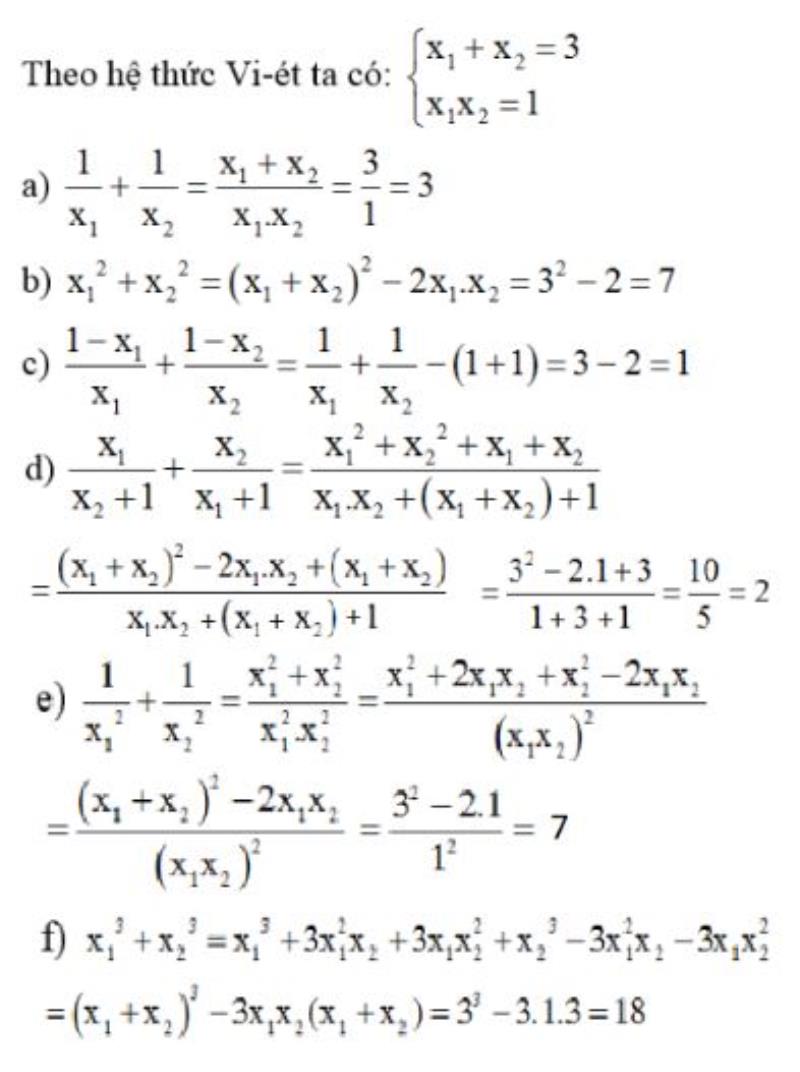
Bài tập 2: Đề bài có phương trình x^2 + (2m – 1)x – m = 0
a. Chứng minh với mọi m phương trình luôn có nghiệm. b. Gọi x1, x2 là 2 nghiệm. Để biểu thức A = \ ( x_1 ^ 2 + x_2 ^ 2 – x_1. x_2 \ ) có giá trị nhỏ nhất hãy tìm giá trị của m.
Bài giải:
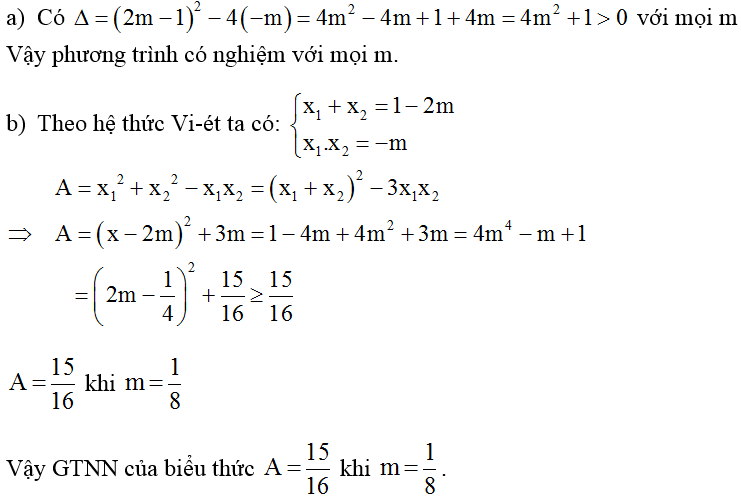
Bài tập 3: Tìm giá trị của k của phương trình x^2 + 2x + k = 0 để nghiệm x1, x2 thỏa mãn 1 trong các điều kiện như sau:
- x1 – x2 = 14
- x1 = 2×2
-
\ ( x_1 ^ 2 + x_2 ^ 2 = 1 \ )
-
1/x1 + 1/x2 = 2
Bài giải:
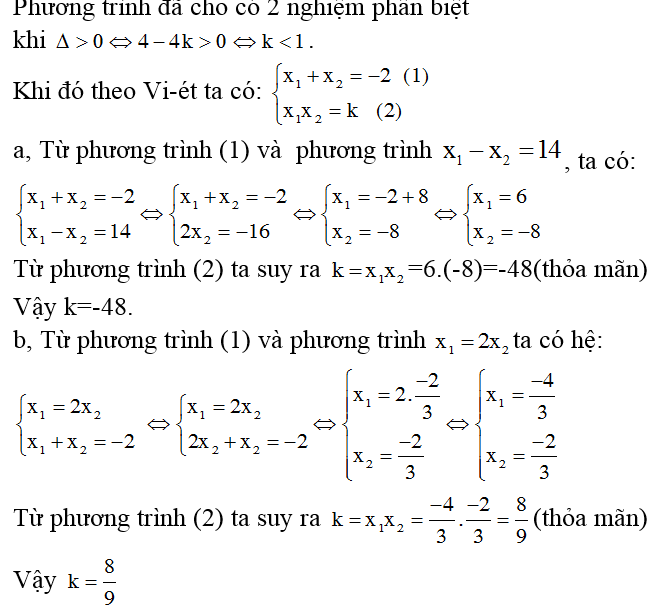
>> Xem thêm:
Source: https://dvn.com.vn
Category: Hỏi Đáp