Lý thuyết nhắc lại và bổ sung các khái niệm về hàm số>

I. Nhắc lại và bổ sung khái niệm về hàm số và đồ thị hàm số

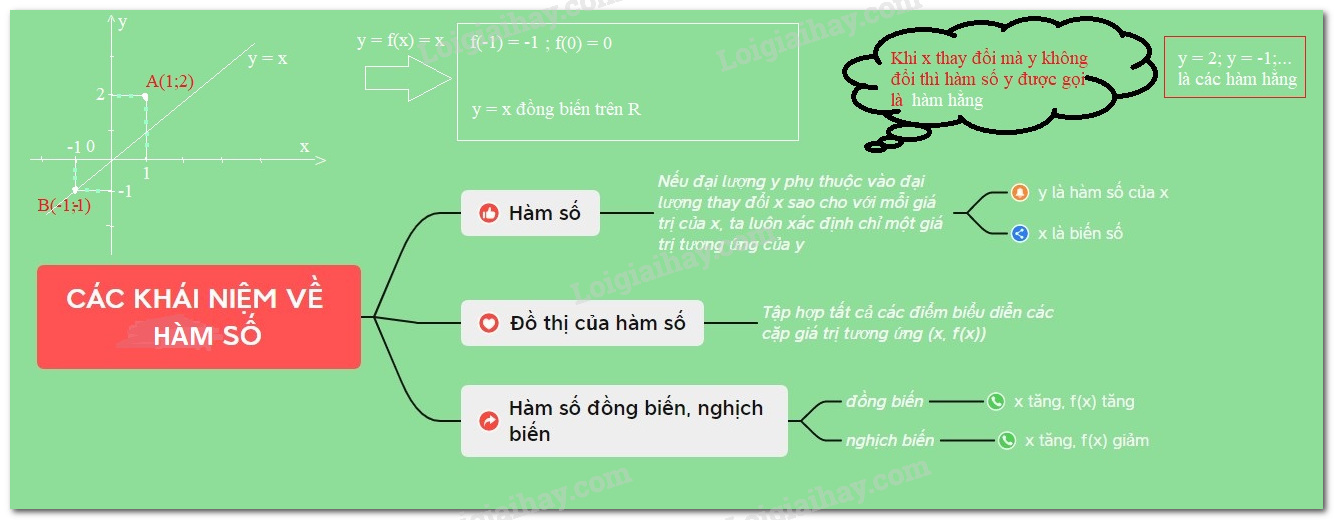
Khái niệm hàm số

+) Nếu đại lượng $y$ phụ thuộc vào đại lượng thay đổi $x$ sao cho với mỗi giá trị của $x$, ta luôn xác định được một và chỉ một giá trị tương ứng của $y$ thì $y$ gọi là hàm số của $x$ ($x$ gọi là biến số).
Ta viết : $y = f\left( x \right)$, $y = g\left( x \right)$, …

+) Giá trị của hàm số $f\left( x \right)$ tại điểm ${x_0}$ kí hiệu là $f\left( {{x_0}} \right)$.

+ ) Tập xác lập USD D $ của hàm số USD f \ left ( x \ right ) USD là tập hợp những giá trị của USD x USD sao cho USD f \ left ( x \ right ) USD có nghĩa .+ ) Khi USD x USD biến hóa mà USD y $ luôn nhận một giá trị không đổi thì hàm số USD y = f \ left ( x \ right ) USD gọi là hàm hằng .

Đồ thị của hàm số

Đồ thị của hàm số USD y = f \ left ( x \ right ) USD là tập hợp toàn bộ những điểm USD M \ left ( { x ; y } \ right ) USD trong mặt phẳng tọa độ $ Oxy $ sao cho USD x, { \ rm { } } y $ thỏa mãn nhu cầu hệ thức $ y = f \ left ( x \ right ) USD

Hàm số đồng biến, nghịch biến
Cho hàm số $y = f\left( x \right)$ xác định trên tập $D$. Khi đó :
– Hàm số đồng biến trên $D $ $\Leftrightarrow \forall {x_1},{x_2} \in D:{x_1} < {x_2} \Rightarrow f\left( {{x_1}} \right) < f\left( {{x_2}} \right)$
– Hàm số nghịch biến trên $D$ $ \Leftrightarrow \forall {x_1},{x_2} \in D:{x_1} < {x_2} \Rightarrow f\left( {{x_1}} \right) > f\left( {{x_2}} \right)$

II. Các dạng toán thường gặp

Dạng 1 : Tính giá trị của hàm số tại một điểm

Phương pháp:

Để tính giá trị $ { y_0 } $ của hàm số USD y = f \ left ( x \ right ) USD tại điểm $ { x_0 } $ ta thay USD x = { x_0 } $ vào USD f \ left ( x \ right ) USD, ta được $ { y_0 } = f \ left ( { { x_0 } } \ right ) USD .

Dạng 2 : Biểu diễn tọa độ của một điểm và xác định điểm thuộc đồ thị hàm số

Phương pháp:

Điểm USD M \ left ( { { x_0 } ; { y_0 } } \ right ) USD thuộc đồ thị hàm số USD y = f \ left ( x \ right ) USD khi $ { y_0 } = f \ left ( { { x_0 } } \ right ) USD

Dạng 3 :  Xét sự đồng biến và nghịch biến của hàm số

Phương pháp:

Bước 1: Tìm tập xác định $D$ của hàm số.

Bước 2 : Giả sử $ { x_1 } < { x_2 } $ và $ { x_1 }, { x_2 } \ in D USD. Xét hiệu $ H = f \ left ( { { x_1 } } \ right ) - f \ left ( { { x_2 } } \ right ) USD . + Nếu USD H < 0 $ với $ { x_1 }, { x_2 } $ bất kể thì hàm số đồng biến . + Nếu USD H > 0 $ với $ { x_1 }, { x_2 } $ bất kể thì hàm số nghịch biến .
Ví dụ : Xét sự đồng biến, nghịch biến của hàm số \ ( y = f ( x ) = 3 x + 1 \ )
Cách giải :
Hàm số xác lập với mọi \ ( x \ in \ mathbb R \ )
Giả sử \ ( { x_1 } < { x_2 } \ ) và \ ( { x_1 }, { x_2 } \ in \ mathbb R \ ) Ta có : \ ( f \ left ( { { x_1 } } \ right ) = 3 { x_1 } + 1 \ ) \ ( f \ left ( { { x_2 } } \ right ) = 3 { x_2 } + 1 \ ) Suy ra \ ( f ( x_1 ) - f ( x_2 ) = 3 x_1 + 1 - ( 3 x_2 + 1 ) \ ) \ ( = 3 ( x_1-x_2 ) < 0 \ ) ( vì \ ( x_ { 1 } < x_ { 2 } \ ) nên \ ( x_ { 1 } - x_ { 2 } < 0 ) \ )

Hay \(f(x_1)
Vậy với \ ( x_ { 1 } < x_ { 2 } \ ) ta được \ ( f ( x_1 ) < f ( x_2 ) \ ) nên hàm số \ ( y = f ( x ) = 3 x + 1 \ ) đồng biến trên \ ( \ mathbb { R } \ ) .

Dạng 4 : Bài toán liên quan đến đồ thị hàm số $y = ax\left( {a \ne 0} \right)$

Phương pháp:

+) Đồ thị hàm số dạng $y = ax{\rm{ }}\left( {a \ne 0} \right)$ là đường thẳng đi qua gốc tọa độ $O$ và điểm $E\left( {1;a} \right)$.

+ ) Cho hai điểm $ A \ left ( { { x_A } ; { y_A } } \ right ) USD và $ B \ left ( { { x_B } ; { y_B } } \ right ) USD. Khi đó độ dài đoạn thẳng $ AB $ được tính theo công thức : USD AB = \ sqrt { { { \ left ( { { x_B } – { x_A } } \ right ) } ^ 2 } + { { \ left ( { { y_B } – { y_A } } \ right ) } ^ 2 } } $ .

Source: https://dvn.com.vn
Category: Hỏi Đáp