Lý thuyết về hai đường thẳng song song>

I. Các kiến thức cần nhớ

1. Khái niệm hai đường thẳng song song

Hai đường thẳng song song ( trong mặt phẳng ) là hai đường thẳng không có điểm chung .

Kí hiệu \(a//b.\)

– Hai đường thẳng phân biệt thì hoặc cắt nhau hoặc song song .

2. Dấu hiệu nhận biết hai đường thẳng song song

+ Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành một cặp góc so le trong bằng nhau thì hai đường thẳng song song .
+ Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành một cặp góc đồng vị bằng nhau thì hai đường thẳng song song .
+ Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành một cặp góc trong cùng phía bù nhau thì hai đường thẳng song song .
Ngoài ra ta còn có tín hiệu : Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành một cặp góc so le ngoài bằng nhau thì hai đường thẳng song song .

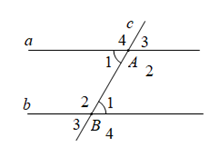
Ví dụ:

+ ) \ ( \ widehat { A_1 } = \ widehat { B_1 } \ )
Mà 2 góc này ở vị trí so le trong
\ ( \ Rightarrow a / / b \ )
+ ) \ ( \ widehat { A_3 } = \ widehat { B_1 } \ )
Mà 2 góc này ở vị trí đồng vị
\ ( \ Rightarrow a / / b \ )
+ ) \ ( \ widehat { A_2 } + \ widehat { B_1 } = { 180 ^ 0 } \ )
Mà 2 góc này ở vị trí trong cùng phía
\ ( \ Rightarrow a / / b \ )

3. Tiên đề Ơ-clít về hai đường thẳng song song

Qua một điểm nằm ngoài một đường thẳng, chỉ có một đường thẳng song song song với đường thẳng đó .

4. Tính chất hai đường thẳng song song

+ Hai góc đồng vị bằng nhau

+ Hai góc trong cùng phía bù nhau

Ví dụ:

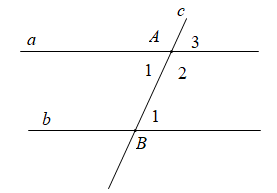Nếu USD a / / b USD thì \ ( \ left \ { \ begin { array } { l } { \ widehat A_1 } = { \ widehat B_1 } \ \ { \ widehat A_3 } = { \ widehat B_1 } \ \ { \ widehat A_2 } + { \ widehat B_1 } = { 180 ^ 0 } \ end { array } \ right. \ )

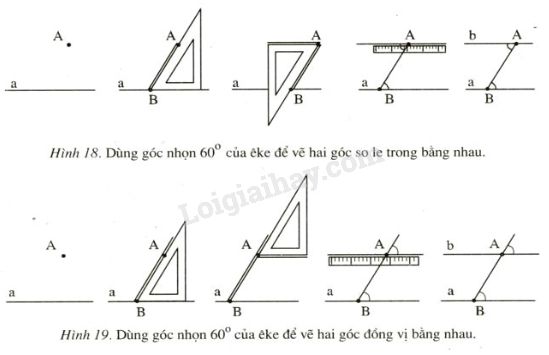
5. Vẽ hai đường thẳng song song

Một số cách vẽ được minh họa như sau :

II. Các dạng toán thường gặp

Dạng 1: Nhận biết và chứng minh hai đường thẳng song song

Phương pháp:

Xét cặp góc so le trong, cắp góc đồng vị hoặc cặp góc trong cùng phía .Rồi sử dụng tín hiệu phân biệt hai đường thẳng song song .

Dạng 2: Tính số đo góc tạo bởi đường thẳng cắt hai đường thẳng song song

Phương pháp:

Sử dụng đặc thù : Nếu hai đường thẳng song song bị cắt bởi một đường thẳng thứ ba thì :+ Hai góc so le trong còn lại bằng nhau+ Hai góc đồng vị bằng nhau+ Hai góc trong cùng phía bù nhau

Dạng 3: Xác định các góc bằng nhau hoặc bù nhau dựa vào tính chất hai đường thẳng song song

Phương pháp:

Bước 1 : Chứng minh hai đường thẳng song song ( nếu chưa có )Bước 2 : Sử dụng đặc thù :

Nếu hai đường thẳng song song bị cắt bởi một đường thẳng thứ ba thì:

+ Hai góc so le trong còn lại bằng nhau+ Hai góc đồng vị bằng nhau+ Hai góc trong cùng phía bù nhau

Source: https://dvn.com.vn
Category: Hỏi Đáp